Konvexität-und-Einfachheit-Test

Für einfache Polygone ist es in linearer Zeit (in Anzahl der Ecken), d.h. in $O(n)$, möglich, festzustellen, ob sie konvex sind oder nicht.

Laufe in irgendeiner Richtung durch die geordnete Punkteliste und überprüfe, ob ein Vorzeichenwechsel bzgl. der Orientierung vorliegt; wenn ja, dann ist das Polygon nicht konvex.

Allerdings hat der zuvor nötige Einfachheit-Test eine Laufzeit von $O(n \log(n))$.

Beides kann zusammen auch in linearer Zeit erfolgen:

1. Führe Vorzeichenwechseltest der Orientierung wie beschrieben durch (d.h. Überprüfen der lokalen Konvexität).
2. Überprüfe, ob mindestens einmal die Orientierung ungleich Null ist und keine Mehrfachecken auftreten.
3. Überprüfe, ob z.B. die $x$-Koordinaten der Ecken jeweils nur ein lokales Maximum und ein lokales Minimum annehmen (d.h. es gibt nur eine Schleife, bzw. das Polygon ist monoton in dieser Richtung).

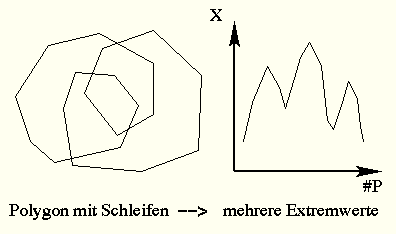
Monotone Polygone sind Polygone mit der Eigenschaft, dass es eine Richtung gibt, so dass jede zu dieser Richtung senkrechte Gerade genau zwei Kanten schneidet.

Stern-konvexe Polygone sind Polygone mit der Eigenschaft, dass es einen inneren Punkt des Polygons gibt, so dass jedes Segment von einem beliebigen Punkt im Innern des Polygons zu diesem Zentrum vollständig innerhalb des Polygons liegt.