Beschleunigungsverfahren bei der Schnittpunktberechnung

Die naive Methode der Schnittpunktsuche führt eine lineare Suche auf allen Objekten der Szene durch, um den nächstgelegenen Schnittpunkt zu finden. Dies kann durch verschiedene Verfahren im Mittel, d.h. für eine Menge von Strahlen, beschleunigt werden.

Einführung von BoundingVolumes:

Man kann den Schnittpunkttest in zwei Phasen unterteilen:

• wird überhaupt getroffen und
• wie ist der exakte Schnittpunkt.

Der erste Punkt muss nicht unbedingt exakt erfolgen, man muss lediglich sicher stellen, dass, wenn der Test `kein Treffer' sagt, dies auch stimmt. Die zweite Phase wird dann eventuell zu oft durchlaufen, aber doch seltener als beim einfachen Verfahren.

Man erreicht dies durch die Einführung von BoundingVolumes, d.h. einfachen geometrischen Körpern, die das eigentliche Objekt möglichst gut umschließen. Man wählt z.B. Kugeln oder achsenparallele Quader.

Um nun zu entscheiden, welches BoundingVolume man benutzt, eignet sich die Definition der Passgenauigkeit:

$$p=\frac{V(\mbox{Originalobjekt})}{V(\mbox{BoundingVolume})}$$

Sei $o$ ein Objekt, $v_o$ ein entsprechendes BoundingVolume. Ferner sei

$n$	die Anzahl der Teststrahlen,
	die das Volumen $v_o$ bei der Darstellung treffen
$B(v_o)$	die Testkosten für einen Strahl mit $v_o$
$m(v_o)$	die Anzahl der Treffer von $o$ in $v_o$ und
$I(o)$	die Schnittkosten für einen Strahl mit $o$

dann lassen sich die Gesamtkosten berechnen mit

$$K(o,v_o)=nB(v_o)+m(v_o)I(o)$$

$m(v_o)$ lässt sich mithilfe von $p$ abschätzen. Ziel ist nun, $K$ durch geeignete Wahl von $v_o$ zu minimieren.

Nutzen von hierarchischen BoundingVolumes:

Trotz der Beschleunigung durch den schnellen Test, ob es sehr wahrscheinlich ist, dass das Objekt getroffen wird, bleibt die Zeit für die Suche nach einem Schnittpunkt linear in der Anzahl der Objekte. Ein Verbesserung--zumindest, wenn man eine Menge von Strahlen betrachtet--erhält man durch hierarchische BoundingVolumes, indem man bereits vorhandene BoundingVolumes wiederum zu größeren BoundingVolumes zusammenfasst.

Das Erstellen dieser Hierarchie kann einerseits

• durch den Benutzer, also in der Szenendefinition, als auch
• automatisch erfolgen.

Quader eignen sich besser als Kugeln zum Aufbau hierarchischer BoundingVolumes, da im Mittel bei der Vereinigung zweier Quader das Volumen des resultierenden Quaders nicht so sehr ansteigt, wie es bei Kugeln der Fall ist.

Die Suchzeit kann pro Strahl weiterhin linear in der Anzahl der Objekte sein kann (man stelle sich die Objekte in einer Art Perlenkette aufgereiht vor).

Die Laufzeit bleibt also im schlechtesten Fall linear, im Mittel ist sie allerdings wesentlich geringer. Da die Verwendung der BoundingVolume auf jeden Fall eine Beschleunigung mit sich bringt, gehen wir in den folgenden Raumunterteilungsverfahren stets davon aus, dass mit BoundingVolumes gearbeitet wird (allerdings nicht notwendigerweise hierarchisch).

Raumunterteilungsverfahren

Unter einer Raumunterteilung verstehen wir die Unterteilung des dreidimensionalen Raumes, in dem sich die Objekte befinden, in kleinere Unterräume. Sind die Unterräume achsenparallele Quader, dann heißen die Unterräume Voxel. Zwei Voxel heißen ähnlich, wenn sie durch gleiche Skalierung der drei Achsen ineinander übergeführt werden können. Sind alle Voxel, die bei einer Aufteilung entstehen, ähnlich, sprechen wir von einer uniformen Unterteilung, im andern Fall von einer nicht-uniformen Unterteilung. Handelt es sich um eine mehrstufige Unterteilung, sprechen wir von einer hierarchischen Unterteilung, sonst von einer nicht-hierarchischen Unterteilung.

Damit ist klar, dass es verschiedene Raumunterteilungsverfahren gibt. Ziel jeder Unterteilung ist es, den Suchraum bei der Schnittpunktberechnung einzuschränken, indem jedem Unterraum nur die in im liegenden Objekte zugeordnet werden (hierzu sind eventuell Kopien notwendig). Durchstreift ein Strahl den Unterraum, brauchen nur diese wenigen Objekte als Kandidaten für einen Schnittpunkt untersucht zu werden.

Um zu verhindern, dass der exakte Schnittpunkt eines Strahls mit einem Objekt mehrfach berechnet wird, wenn das Objekt mehrere Voxel schneidet, merkt man sich Strahlnummern und die zuletzt berechneten Schnittpunkte. Vor einer erneuten Schnittpunktberechnung testet man nun zuerst die Strahlnummer mit dem aktuellen Strahl und spart sich so eine erneute Berechnung. Weiterhin muss man darauf achten, dass der Schnittpunkt im aktuellen Voxel liegt. Dies ist eine notwendige Bedingung für den nächsten Schnittpunkt.

Bemerkung: Die hier verwendeten Definitionen entsprechend nicht den in der Literatur sonst üblichen Definitionen. Dort wird meist das, was hier hierarchisch ist, als nicht-uniform und das, was hier nicht-hierarchisch ist, als uniform bezeichnet.

Die Beschreibung enthält stets eine grobe Abschätzung des Aufwandes, der bei der Schnittpunktberechnung notwendig ist. Dabei wird immer von einer regelmäßigen oder zufälligen Anordnung vieler relativ kleiner Objekte ausgegangen. Zufällig soll hier nicht formal eingeführt werden, sondern damit soll lediglich gesagt werden, dass man erwartet, in einem beliebigen, nicht zu kleinen, aber konstantem Raumvolumen im Wesentlichen die gleiche Anzahl von Objekten vorzufinden, die diesen Unterraum schneiden.

Die Anzahl der Objekte der Szene sei $n$. Müssen durch die Raumunterteilung Objektinformationen kopiert werden, so bezeichne $k$ den Faktor, um den sich die Objektinformation erhöht. Als Beispiel nehme man an, dass jedes Voxel einen Zeiger auf jedes Objekt enthält, welches das Voxel schneidet. Müssen 10 % der Zeiger dupliziert werden, ist $k=1.1$. Desweiteren sei $d$ die Anzahl der Unterräume, die ein Strahl im Mittel trifft, wenn er die Szene durchläuft.

Grid:

Der Raum, den die Szene einnimmt, wird durch ein Grid in gleich große Voxel eingeteilt. Übliche Einteilungen verwenden bis zu $10\times 10\times 10$ Voxel, d.h. es entstehen 1000 Unterräume. Jedem Voxel werden die dieses Voxel schneidenden Objekte (deren BoundingVolumes) zugeordnet. Schneidet ein Objekt mehr als ein Voxel, muss es also in mehreren Voxeln gehalten werden (zumindest ein Verweis auf das Objekt).

Die Schnittpunktsuche beginnt in dem Voxel, das den Aufpunkt des Strahles enthält. Trifft er kein Objekt innerhalb des Voxels, wird das nächste Voxel mithilfe eines modifizierten BRESENHAM-Algorithmus bestimmt und die Suche dort fortgesetzt.

Grobe Abschätzung des Berechnungsaufwandes:

Gehen wir von $c^3$ vielen Voxeln aus. In jedem Voxel liegen dann $k*n/c^3$ viele Objekte. Für einen Strahl sind im Mittel $d$ Voxel zu testen. Bei einer Durchquerung der Szene können höchstens $3c$ viele Voxel geschnitten werden. Für sehr dicht besetzte Szenen kann man davon ausgehen, dass die Anzahl der durchquerten Voxel unabhängig von $c$ ist; die Anzahl der geschnittenen Voxel kann dann sogar als Konstante auftreten.

Als Berechnungszeit für die Schnittpunktbestimmung ergibt sich also zu

$$O(dk\frac{n}{c^3})$$

und somit im schlechtesten Fall (alle Objekte schneiden alle Voxel) zu

$$O(3cn)$$

Die Methode lohnt sich also nur dann, wenn gilt:

$$dk<c^3$$

Der Aufwand zum Finden der Voxel, die der Strahl schneidet, ist $O(d)$ somit höchstens $O(c)$.

Im Falle $c=8$, $k=1.1$ und $d=3$ ergibt sich also eine Reduzierung auf das 0.0065-fache der Zeit der naiven linearen Testmethode. Hierbei wurden weitere Konstanten vernachlässigt. Allerdings sind diese nicht wesentlich größer als bei der linearen Suche, da man genau diese innerhalb der Voxel auch benutzt und das Finden der Voxel mithilfe des BRESENHAM-Algorithmus sehr schnell geht.

Der Speicherplatz erhöht sich linear, da für jedes Objekt ein Verweis in mindestens einem Voxel gehalten werden muss. Sind allerdings Kopien notwendig, erhöht sich der Platz auf $O(kn)$, was im schlechtesten Fall zu $O(c^3n)$ führen kann.

Lattice:

Hier wird der Raum analog zum Grid in quaderförmige Unterräume eingeteilt. Allerdings findet diese Unterteilung nicht an festen Stellen statt, sondern die Objektgrenzen werden berücksichtig. Dies führt dazu, dass man durch eine günstige Platzierung der Schnittebenen weniger Objekte schneidet und somit auch weniger Objektinformation kopieren muss, d.h. $k$ ist geringer als beim Grid. Die Anzahl der im Mittel von einem Strahl geschnittenen Quader ist ebenfalls nicht höher als beim Grid.

Die Laufzeitabschätzung ist ähnlich der des Grid, nun jedoch mit unterschiedlichen Einteilungen in den drei Raumrichtungen. Man erhält also

$$O(dk\frac{n}{c_xc_yc_z})$$

und somit im schlechtesten Fall (alle Objekte schneiden alle Voxel)

$$O((c_x+c_y+c_z)n)$$

Die Methode lohnt sich also nur dann, wenn gilt:

$$dk<c_xc_yc_z$$

Wie gesagt, man erwartet ein kleineres $k$ als beim Grid und zudem lassen sich in nicht regelmäßigen, clusterartigen Szenen gute Aufteilungen des Raumes finden.

Für den BRESENHAM-Algorithmus müssen nun auch die Intervallängen der Einteilungen in X-, Y- und Z-Richtung gespeichert werden, was den Platzbedarf um $O(c_xc_yc_z)$ erhöht (was bei vielen Objekten vernachlässigt werden kann). Ansonsten steigt der Platzbedarf wie beim Grid.

Octree:

Der Raum wird durch wiederholte Halbierung der Kanten des die Szene umgebenden achsenparallelen Quaders in immer kleinere Quader unterteilt. Wird diese Unterteilung balanciert ausgeführt, haben alle Voxel die gleiche Größe (weshalb ich es--im Gegensatz zur Literatur--als uniforme Raumunterteilung bezeichne). Normalerweise wird eine weitere Unterteilung eines Unterraumes abgebrochen, sobald die Anzahl der Objekte innerhalb eines Voxels eine bestimmte Untergrenze unterschreitet, d.h. hinreichend leere Voxel werden nicht weiter unterteilt.

Die Abbildung zeigt einen Quadtree (das zweidimensionale Analogon) mit der Abbruchbedingung, dass keine weitere Unterteilung im Falle von zwei Objekten im Unterraum stattfindet.

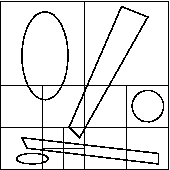
Wiederum werden jedem Voxel als Blatt im Baum `seine' Objekte mitgeteilt. Dies bedeutet, dass ebenfalls Information kopiert werden muss, wenn ein Objekt mehrere Voxel schneidet.

Wenn sich Objekte überlappen können, muss ein weiteres Kriterium als Rekursionsabbruch beim Aufbau des Octree berücksichtigt werden, da die vorgegebene minimale Anzahl nicht notwendigerweise erreicht werden muss: es kann vorkommen, dass eine weitere Unterteilung keine Reduktion der Objektanzahl in einem Voxel mit sich bringt.

Als mögliche Kriterien können z.B. genutzt werden:

• Durch die Unterteilung sinkt die Anzahl der Objekte in einem Unterraum nicht auf mindestens einen vorgebenen Prozentsatz des Oberraumes.
  
  $$\char93 \mbox{Obj}_{\mbox{Unterraum}}\geq s*\char93 \mbox{Obj}_{\mbox{Oberraum}} \quad\mbox{mit}\quad 0<s<1$$
  
  

• Durch die Unterteilung steigt die Summe aller Objekte in den Unterräumen auf mehr als ein vorgegebenes Vielfaches der Anzahl im Oberraum.
  
  $$\sum\char93 \mbox{Obj}_{\mbox{Unterraum}}\geq s*\char93 \mbox{Obj}_{\mbox{Oberraum}} \quad\mbox{mit}\quad 1<s<8$$
  
  

Die Schnittpunktberechnung startet wieder in dem Voxel, welches den Aufpunkt des Strahles enthält. Dieses wird durch einen `top-down'-Lauf durch den Baum gefunden. Das Auffinden des nächsten Voxel, das der Strahl beim Verlassen des vorhergehenden betritt, wird wie folgt gefunden:

1. Bestimmen eines Punktes, der innerhalb dieses Voxels liegt und
2. Suchen des Voxel mithilfe dieses Punktes

Eine mögliche Implementierung dieser beiden Schritte arbeitet wie folgt:

1. Man bestimmt den Schnittpunkt des Strahls mit der Oberfläche des aktuellen Voxel oder auch nur die Seitenfläche, die getroffen wird. Nun wählt man einen Punkt außerhalb des aktuellen Voxel in der dominanten Strahlrichtung, der die halbe, minimale Voxelausdehnung entfernt liegt. Dies kann entweder vom gefundenen Wandschnittpunkt (Sonderfall der Kanten muss man berücksichtigen) oder vom Zentrum der Seitenfläche aus erfolgen. Dieser Punkt liegt nun mit Sicherheit im nächsten getroffenen Voxel.

2. Das entsprechende Voxel findet man nun wieder durch einen `top-down'-Lauf durch den Baum. Ist $d$ sehr klein, d.h. die Strahlen legen im Mittel nur kleine Wege in der Szene zurück, lohnt es sich, erst im Baum ein Stück noch oben zu suchen, bis man das Voxel gefunden hat, das sowohl den Aufpunkt als auch den neuen Punkt enthält, und dann abwärts dasjenige Voxel sucht, das nur den neuen Punkt enthält.

Grobe Abschätzung des Berechnungsaufwandes:

Sei $c$ die Baumtiefe des Octree. Da die Objekte regelmäßig/zufällig verteilt sind, ist der Baum im Wesentlichen balanciert. Es gibt somit $2^{3c}$ Voxel als Blätter, die Objektinformation enthalten müssen. Sei $k$ der Faktor auf den sich die Objektanzahl bei der Unterteilung eines Voxel erhöht. Für einen Baum der Tiefe $c$ erhöht sich die Objektanzahl auf

$$n+(k-1)n+2(k-1)n+\dots+2^{c-1}(k-1)n = ((2^c-1)(k-1)+1)n$$

wenn man annimmt, dass jede Schnittebene in der Szene die gleiche Anzahl von Objekten schneidet. In jedem Voxel als Blatt liegen also

$$\frac{((2^c-1)(k-1)+1)n}{2^{3c}}$$

Objekte und als Laufzeit ergibt sich

$$O(d\frac{((2^c-1)(k-1)+1)n}{2^{3c}})$$

Mit der gleichen Argumentation wie beim Grid werden $d$ Voxel als Blätter von einem Strahl durchlaufen.

Für jeden Voxel muss ein `top-down'-Lauf durch den Baum implementiert werden, was langsamer als ein Auffinden des nächsten Voxel mithilfe des BRESENHAM-Algorithmus ist: man erhält $O(d*c)$, also als Maximum mit $d=3*2^c$ ergibt sich $O(c2^c)$.

Ist die Anzahl der Voxel als Blätter des Octree gleich der Anzahl der Voxel im Grid, dann ergeben sich die gleichen Laufzeiten bei der Schnittpunktsuche. Nur im Auffinden des nächsten geschnittenen Voxels verliert man mehr Zeit beim Octree als beim Grid. Der Faktor $k$ des Grid entspricht dem Faktor $((2^c-1)(k-1)+1)$ des Octree, da die Blätter des Octree den Raum analog zu einem Grid aufteilen.

Somit ist klar, dass der Octree dem Grid nicht überlegen ist, wenn es sich um regelmässige/zufällige Szenen handelt. Der Octree gewinnt erst, wenn es sich um unregelmäßige, clusterartige Objektansammlungen handelt und man durch den Octree schnell große Raumbereiche durchdringen kann. In diesem Fall ist es möglich--durch nicht balancierte Bäume--die Zahl der in einem Blatt gespeicherten Objekte für alle Voxel als Blätter eher gleich zu halten oder auch sehr klein.

BSP-tree:

Der `binary space partition tree' entspricht dem Octree, allerdings wird die Unterteilung der Quader ähnlich wie beim Lattice anhand von Objektgrenzen durchgeführt. Man versucht durch jede Unterteilung links und rechts der Schnittebene die gleiche Anzahl von Objekten zu erhalten und die Anzahl der zu duplizierenden Objekte gering zu halten. Man unterteilt also nicht notwendigerweise stets abwechselnd in den drei Raumdimensionen.

Die Schnittpunktsuche erfolgt analog zu dem Verfahren, wie es für den Octree beschrieben worden ist. Die Laufzeitabschätzung für einen BSP-tree entspricht bei der vorgegebenen Szenenbeschreibung der des Octree, da aufgrund der Objektverteilung die Schnittebenen mehr oder weniger an die gleiche Stelle gelegt werden.

Ein BSP-tree hat also auch nur den Vorteil, eine gleichmäßigere Aufteilung der Objekte auf die Voxel als Blätter zu ermöglichen. Dies erweist sich jedoch bei clusterartigen Objektanordnungen als deutlicher Vorteil.

Uni-tree:

In einem Voxel bei Grid oder Lattice bzw. in einem Voxel als Blatt bei Octree oder BSP-tree bleibt die Anzahl der Objekte beschränkt. Die Frage stellt sich, wie man dort den Schnittpunkt findet, wenn es mehr als ein Objekt enthält. Es stehen folgende Möglichkeiten zur Verfügung:

• lineare Suche,
• hierarchische BoundingVolumes und
• PlaneTraversal.

PlaneTraversal arbeitet wie folgt. Jede Seitenfläche eines BoundingVolumes (wir setzen Quader als BoundingVolumes voraus) definiert eine Ebene. Man erhält also $6*\char93 \mbox{Objekte}$ viele Ebenen. Jede Ebene kennt ihr Objekt. Die Ebenen sind entsprechend ihrer Koordinate sortiert. Der Strahl durchläuft das Voxel--dabei werden die Ebenen geschnitten--und aktiviert bzw. deaktiviert ein entsprechendes Bit je Koordinate pro BoundingVolume je nachdem, ob das BoundingVolume des Objektes potentiell in dieser Koordinate betreten oder verlassen wird. Sind alle drei Bits aktiviert, wird das BoundingVolume getroffen und ein Schnittpunkttest kann erfolgen. Man kann die Suche abbrechen, sobald eine Ebene getroffen wird, die hinter dem letzten gefundenen Schnittpunkt liegt.

Da dieses Verfahren sehr effizient implementiert werden kann, arbeitet es bis zu einer gewissen Objektanzahl schneller als ein Verfahren mit hierarchischen BoundingVolume.

Überlappen sich BoundingVolume stark, ist es nicht unbedingt sinnvoll ein übergeordnetes BoundingVolume zu konstruieren, da für die meisten Strahlen sowieso beide getestet werden müssen. In diesem Fall erweitert man die hierarchische BoundingVolume-Struktur dadurch, dass man an den Knoten mehr als zwei Söhne zulässt. Bei der Schnittpunktsuche muss dann jedoch stets die gesamte Liste der Söhne durchsucht werden. Dies kann jedoch wiederum schnell mit PlaneTraversal erfolgen.

Eine einfache Modifizierung des Octree, die nicht nur 8 Unterräume pro Unterteilung eines Voxels erzeugt und damit eventuell Objektinformation kopieren muss, besteht darin, alle durch Schnittebenen des Octree (oder auch eines BSP-tree) geschnittenen Objekte in ein eigenes Voxel (Universum) zusammenzufassen. Dabei können also je Unterteilungsschritt bis zu 27 Unterräume entstehen. (In jedem Unterraum sind die Objekte zusammengefasst, die durch die gleichen Schnittebenen des Octree geschnitten werden.)

Man beachte, dass sich nun die entstandenen Voxel durchdringen können, und man somit das oben erläuterte Verfahren mit sich überlappenden BoundingVolumes nutzen muss.

Direction-tree:

Der `direction tree' ist ein Unterteilungsverfahren, welches man ebenfalls unter uniforme Raumunterteilung einordnen kann. Der Raum wird jedoch nicht einfach in Voxel unterteilt, sondern man macht sich die Tatsache zu nutzen, dass ein Strahl nur 5 Freiheitsgrade hat. Er lässt sich nämlich durch seinen Aufpunkt (drei Werte) und seine Richtung in Polarkoordinaten (zwei Werte) beschreiben. Da man geeigneter Weise keine Polarkoordinaten sondern $(u,v)$-Werte auf einer umgebenden Oberfläche (Würfel) nimmt, ergibt sich als weiterer Freiheitsgrad eine der sechs Hauptachsenrichtungen.

Die Raumunterteilung erfolgt nun rekursiv, abwechselnd in den fünf Dimensionen. Die Hauptachsenrichtung spielt natürlich auch eine Rolle und bewirkt eine Multiplikation mit 6. In den ersten drei Dimensionen entstehen Voxel analog zum Octree-Verfahren. In den anderen beiden Dimensionen entstehen Pyramiden. Die Objekte werden wiederum jedem Raumbereich zugeordnet. In den Pyramiden werden die Objekte zusätzlich in der Richtung der Pyramide sortiert, so dass der nächstgelegene Schnittpunkt schneller gefunden werden kann.

Das Verfahren traversiert also den entstehenden Baum und bestimmt jeweils in welchen Raumbereich der Strahl fällt. An einem Blatt wird dann der Schnittpunkt berechnet. Der Speicherplatzverbrauch dieser Methode ist erheblich, da sich die Pyramiden deutlich überlappen. Man kann fast sagen, dass jedes nur durch die ersten drei Raumdimensionen erzeugte Voxel den gesamten Objektraum sieht, d.h. die Anzahl der Blätter eines Octree (bezüglich der X-, Y- und Z-Koordinate entsteht gerade ein Octree) bestimmt, wie oft die Objektinformationen kopiert werden müssen, da man von einem solchen Voxel, den gesamten Raum sehen kann. Eine Reduzierung erhält man durch einen adaptiven Aufbau der Datenstruktur mit `caching'-Strategien (`lazy evaluation'). Einen interessanten Beschleunigungseffekt erhält man auch durch die Begrenzung der Ausdehenung der Pyramiden. Jeder Raumpunkt sieht praktisch nur eine gewisse Distanz weit, d.h. für jeden Punkt können sehr weit entfernte Objekte vernachlässigt werden. Bei den Lichtquellen wurde diese Methode weiter oben bereits vorgestellt: es wird nur das erste getroffene Objekt in einem Raumwinkel gespeichert, da alle dahinterliegenden automatisch in Schatten liegen.

Als grobe Laufzeitanalyse erhält man, wiederum für eine große Anzahl regelmäßig/zufällig verteilter, kleiner Objekte:

Wir nehmen an, dass der Baum balanciert aufgebaut ist. Dann liegen in jeder Pyramide etwa gleich viele Objekte. Sei $k$ wiederum der Faktor, der angibt um wieviel die Anzahl der Objekte vergrößert werden muss, wenn eine Unterteilung in allen fünf Dimensionen erfolgt ist. Wir nehmen der Einfachheit wegen an, dass in jedem Rekursionsschritt die Anzahl der Objektinformationen um den gleichen Faktor $k$ steigt.

Sei $c$ die Tiefe des Baumes, wobei in jeder Dimension unterteilt worden ist. Mit jedem Rekursionsschritt wächst die Anzahl der Blätter also um den Faktor $2^5=32$. In einer Pyramide als Blatt liegen also

$$O(\frac{k^c}{2^{5c}}n)$$

Objekte.

Bei der Schnittpunktberechnung wird ein Pfad des Baumes mit Länge $5c$ (wegen der Unterteilung in allen Dimensionen) durchlaufen, allerdings braucht nur ein Blatt untersucht zu werden, da der Strahl ganz in einer Pyramide verläuft. Man erhält also:

$$O(2^{c(\log k-5)}n)$$

als Laufzeit. Die Bestimmung der Hauptachsenrichtung taucht nur als Konstante in jedem Knoten des Pfades auf. Bei einer Tiefe $c=3$ (entspricht 32768 Blättern) und einer Überlappung von $k=8$ beträgt die Beschleunigung $0.0156$.