



Nächste Seite: Transparenz
Aufwärts: Sichtbarkeitsberechnungen
Vorherige Seite: Tiefenpuffermethode
Inhalt
Zur Beschleunigung der Berechnung der  -Werte kann
ein Scanline-Algorithmus (ähnlich wie beim Füllen von Polygonen
vorgestellt) unter Zuhilfenahme einer differentiellen Methode angewendet
werden.
-Werte kann
ein Scanline-Algorithmus (ähnlich wie beim Füllen von Polygonen
vorgestellt) unter Zuhilfenahme einer differentiellen Methode angewendet
werden.
Betrachten wir den einfachen Fall einer rechtwinkligen Parallelprojektion,
wobei das Sichtvolumen so normiert wurde, dass die  - und
- und
 -Koordinaten gerade den Bildebenenkoordinaten entsprechen.
-Koordinaten gerade den Bildebenenkoordinaten entsprechen.
Ebenengleichung eines Polygons:
Damit erhalten wir die  -Koordinate für den Bildpunkt
-Koordinate für den Bildpunkt 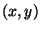 als:
als:
und für 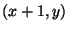
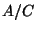 ist eine Konstante für das ganze Polygon.
ist eine Konstante für das ganze Polygon.
Die Kanten des Polygon zeichnet man z.B. mit einem Bresenham-Verfahren.
Der Algorithmus kann mit folgenden ``Tricks'' weiter
verbessert werden:
- Man arbeitet generell mit einem Scanline-Verfahren.
- Man sortiert die Ecken der Polygone bzgl. ihrer
 -Koordinaten
der Projektion.
-Koordinaten
der Projektion.
- Man bearbeitet nur die Polygone, die gerade von der aktuellen
Scanline geschnitten werden, d.h. man hält sich eine
Liste von aktiven und inaktiven Polygonen, die nach jeder
Scanline aktualisiert wird.
- Man kann also mit einem kleineren Ausschnitt eines
 -Puffers
arbeiten (z.B. mit einigen scanlines statt
mit dem gesamten Bild).
-Puffers
arbeiten (z.B. mit einigen scanlines statt
mit dem gesamten Bild).
- Die Reihenfolge der Durchmusterung der Objekte ist prinzipiell
unerheblich, sie kann sich deshalb an anderen Kriterien orientieren,
z.B. an der Minimierung von Zustandsänderungen des Systems
- Das Verfahren ist nicht dafür geeignet,
transparente Objekte korrekt darzustellen.




Nächste Seite: Transparenz
Aufwärts: Sichtbarkeitsberechnungen
Vorherige Seite: Tiefenpuffermethode
Inhalt
© 2004/2005, A. Formella & D. Fellner, Universität Braunschweig
![]() -Werte kann
ein Scanline-Algorithmus (ähnlich wie beim Füllen von Polygonen
vorgestellt) unter Zuhilfenahme einer differentiellen Methode angewendet
werden.
-Werte kann
ein Scanline-Algorithmus (ähnlich wie beim Füllen von Polygonen
vorgestellt) unter Zuhilfenahme einer differentiellen Methode angewendet
werden.
![]() - und
- und
![]() -Koordinaten gerade den Bildebenenkoordinaten entsprechen.
-Koordinaten gerade den Bildebenenkoordinaten entsprechen.
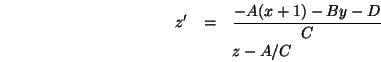
![]() ist eine Konstante für das ganze Polygon.
ist eine Konstante für das ganze Polygon.