



Nächste Seite: Tiefenpuffer mit Scanline-Methode
Aufwärts: Sichtbarkeitsberechnungen
Vorherige Seite: Elimination der Rückseiten
Inhalt
Man spricht auch von 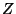 -Puffermethode
(z-buffer- oder depth-buffer-method),
da üblicherweise die
Blickrichtung der
-Puffermethode
(z-buffer- oder depth-buffer-method),
da üblicherweise die
Blickrichtung der  -Richtung entspricht (damit steht
-Richtung entspricht (damit steht  und
und
 für die Bildebene zur Verfügung).
für die Bildebene zur Verfügung).
Idee: Halte für jeden Bildschirmpunkt zusätzlich
einen  -Wert, der den bzgl. der Kamera (genauer Bildebene) berechneten
Abstand kodiert. Ein Pixel wird nur dann aktualisiert, wenn der
entsprechende Punkt des zu
zeichnenden Objektes für dieses Pixel einen Abstand näher zur
Kamera aufweist.
-Wert, der den bzgl. der Kamera (genauer Bildebene) berechneten
Abstand kodiert. Ein Pixel wird nur dann aktualisiert, wenn der
entsprechende Punkt des zu
zeichnenden Objektes für dieses Pixel einen Abstand näher zur
Kamera aufweist.
Man beachte, dass dies das intuitive Verständnis ist;
man kann z.B. natürlich die Vergleiche invertieren oder
andere Spezialeffekte mit der Methode implementieren.
Ist das Sichtvolumen normiert, d.h. die Bildebene hat  -Koordinate
gleich 0 und die hintere Begrenzungslinie hat eine
-Koordinate
gleich 0 und die hintere Begrenzungslinie hat eine  -Koordinate gleich 1,
dann sieht der Algorithmus (für Polygone) wie folgt aus:
-Koordinate gleich 1,
dann sieht der Algorithmus (für Polygone) wie folgt aus:
- Initialisiere den
 -Puffer mit 1.
-Puffer mit 1.
- Zeichne die zu setzenden Pixel der projizierten Polygone
in irgendeiner Reihenfolge, berechne dabei
- den Abstand zur Bildebene und
- überschreibe ein Pixel nur dann, wenn der Abstand
kleiner als der aktuelle Abstand für dieses
Pixel im
 -Puffer ist
-Puffer ist
Eigenschaften:
- leicht zu implementieren
- arbeitet prinzipiell für beliebige Objekte
(lediglich kann es aufwendiger werden, die entsprechende
 -Koordinate eines Pixels zu berechnen)
-Koordinate eines Pixels zu berechnen)
- funktioniert für jede Art der
Projektion (insbesondere bei normiertem Sichtvolumen).
- je nach Genauigkeit für die Speicherung der
 -Werte
und die Größe des Bildes hoher Speicherplatzverbrauch
für den
-Werte
und die Größe des Bildes hoher Speicherplatzverbrauch
für den  -Puffer
-Puffer
- es kann aufgrund der Genauigkeit der gespeicherten
 -Werte
zu nicht korrekt durchgeführten Vergleichen kommen
-Werte
zu nicht korrekt durchgeführten Vergleichen kommen
- bei Anwendung einer perspektivischen Division ist das kanonische
Sichtvolumen häufig uniform in
 -Richtung unterteiltt,
wodurch die äquidistante
Einteilung des Sichtvolumens einer nicht-äquidistanten Einteilung
des Raumes entspricht
-Richtung unterteiltt,
wodurch die äquidistante
Einteilung des Sichtvolumens einer nicht-äquidistanten Einteilung
des Raumes entspricht
- heutige Grafikkarten unterstützen den
 -Puffer in Hardware
-Puffer in Hardware




Nächste Seite: Tiefenpuffer mit Scanline-Methode
Aufwärts: Sichtbarkeitsberechnungen
Vorherige Seite: Elimination der Rückseiten
Inhalt
© 2004/2005, A. Formella & D. Fellner, Universität Braunschweig
![]() -Puffermethode
(z-buffer- oder depth-buffer-method),
da üblicherweise die
Blickrichtung der
-Puffermethode
(z-buffer- oder depth-buffer-method),
da üblicherweise die
Blickrichtung der ![]() -Richtung entspricht (damit steht
-Richtung entspricht (damit steht ![]() und
und
![]() für die Bildebene zur Verfügung).
für die Bildebene zur Verfügung).
![]() -Wert, der den bzgl. der Kamera (genauer Bildebene) berechneten
Abstand kodiert. Ein Pixel wird nur dann aktualisiert, wenn der
entsprechende Punkt des zu
zeichnenden Objektes für dieses Pixel einen Abstand näher zur
Kamera aufweist.
-Wert, der den bzgl. der Kamera (genauer Bildebene) berechneten
Abstand kodiert. Ein Pixel wird nur dann aktualisiert, wenn der
entsprechende Punkt des zu
zeichnenden Objektes für dieses Pixel einen Abstand näher zur
Kamera aufweist.
![]() -Koordinate
gleich 0 und die hintere Begrenzungslinie hat eine
-Koordinate
gleich 0 und die hintere Begrenzungslinie hat eine ![]() -Koordinate gleich 1,
dann sieht der Algorithmus (für Polygone) wie folgt aus:
-Koordinate gleich 1,
dann sieht der Algorithmus (für Polygone) wie folgt aus: