la transformada de Fourier es una herramienta imprescindible cuando
se trabaja con señales periódicas, es decir, con
![]() ,
, ![]() y
y
![]() siendo una función
siendo una función ![]() -periódica sobre
-periódica sobre ![]() podemos
representar la función
podemos
representar la función ![]() con la suma
con la suma
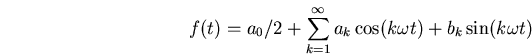
donde los coeficientes se calcula como
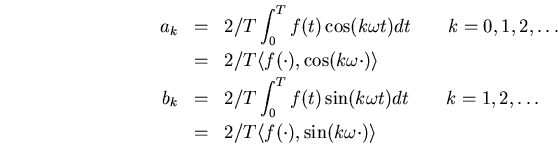
la suma con el argumento ![]() se puede expresar también con
el argumento en
se puede expresar también con
el argumento en ![]() (notando el eje imaginario con
(notando el eje imaginario con ![]() )
que nos lleva a
)
que nos lleva a

nota que la sumación se realiza ahora con índices sobre todo ![]()
la equivalencia de ambos formas en el caso de funciones ![]() reales
vemos aprovechando de la ecuación de Euler
reales
vemos aprovechando de la ecuación de Euler
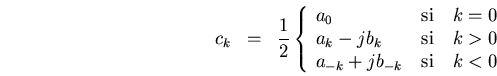
mostrámoslo

las funciones exponenciales complejas forman un sistema ortogonal
sobre ![]() (ya lo mostramos gráficamente en el caso de las funciones harmónicas
(ya lo mostramos gráficamente en el caso de las funciones harmónicas
![]() y
y ![]() ) como se comprueba fácilmente:
) como se comprueba fácilmente:

para los coeficientes ![]() tenemos entonces
tenemos entonces
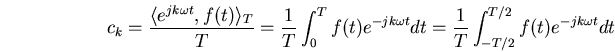
que reproducen las fórmulas para los ![]() y
y ![]() dados arriba
dados arriba
las funciones exponenciales complejas forman también
una base del ![]() que no comprobamos aquí
que no comprobamos aquí
muchas señales que se encuentran en la práctica no son
periódicas (p.ej. señal de voz o música), es decir, el periódo
![]() tiende hacia
tiende hacia ![]()
si realizamos el paso
![]() obtenemos la transformada de
Fourier donde la frecuencia es una variable continua, detallamos:
obtenemos la transformada de
Fourier donde la frecuencia es una variable continua, detallamos:
resustituimos ![]()
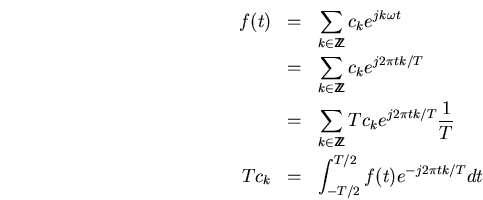
si replazamos ![]() por
por ![]() y si aprovechamos de
y si aprovechamos de
![]() obtenemos
obtenemos
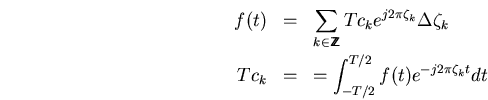
es decir, ![]() depende de
depende de ![]() ,
, ![]() y
y ![]() y lo podemos expresar
con un operador sobre
y lo podemos expresar
con un operador sobre ![]() que depende de
que depende de ![]() y trabaja con
y trabaja con ![]()
entonces tenemos
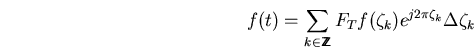
con el paso
![]() las variables
las variables ![]() se conviertan
en una variable
se conviertan
en una variable ![]() continua y obtenemos para los coeficientes
y la serie (escribiendo
continua y obtenemos para los coeficientes
y la serie (escribiendo ![]() para
para ![]() )
)
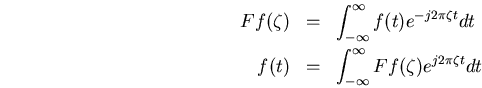
la función ![]() se llama transformada de Fourier de
se llama transformada de Fourier de ![]()
en algunos textos se usa en vez de ![]() la frecuencia angular
la frecuencia angular ![]() para expresar la transformada de Fourier,
con
para expresar la transformada de Fourier,
con
![]() se conviertan las expresiones en
se conviertan las expresiones en
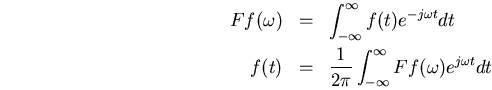
calculamos, por ejemplo, la transformada de Fourier de la función de escalado de Haar
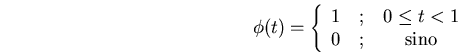
es decir
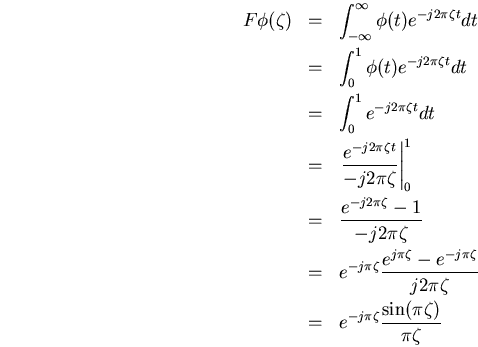
(el último paso se realiza con la ecuación de Euler)
asumimos que las funciones ![]() y
y ![]() abajo tengan transformadas
de Fourier y que pertenezcan a
abajo tengan transformadas
de Fourier y que pertenezcan a
![]() , entonces
la transformada de Fourier tiene las siguientes propriedades
(usando de nuevo
, entonces
la transformada de Fourier tiene las siguientes propriedades
(usando de nuevo ![]() para indicar que la ecuación es
valida para todos los posibles argumentos):
para indicar que la ecuación es
valida para todos los posibles argumentos):


es un buen ejercicio comprobar las propriedades