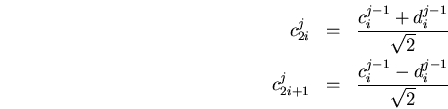las ecuaciones que usamos para calcular la transformada de Haar fueron:

si colocamos los coeficientes para un índice ![]() en una secuencia de valores,
es decir,
en una secuencia de valores,
es decir,

podemos describir el análisis (el paso de ![]() a
a ![]() )
como un filtrado digital:
)
como un filtrado digital:

donde ![]() calcula la media y
calcula la media y ![]() los detalles, más preciso
los detalles, más preciso
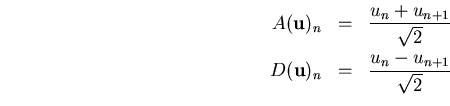
igualmente se puede escribir la reconstrucción (el paso de
![]() a
a ![]() ) como un filtrado digital con sumación:
) como un filtrado digital con sumación:
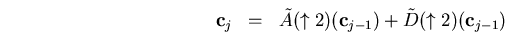
donde ![]() y
y ![]() calculan
calculan
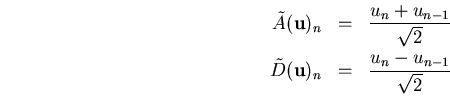
veremos que ...