Equivalencia y ambigüedad

Dos gramáticas son equivalentes si generan el mismo lenguaje, es decir, $G_1\equiv G_2$ si $L(G_1)=L(G_2)$.

(Adelanto: averiguar en general si dos gramáticas son equivalentes es un problema no computable.)

Sea $G=(\{\$,A\},\{1\},\{\$\longrightarrow 1A,\$\longrightarrow 11,A\longrightarrow 1\},\$)$ una gramática. Tanto $\$\longrightarrow 11$ como $\$\longrightarrow 1A \longrightarrow 11$ es una derivación para la palabra $11$.

Una sentencia es ambigua si existen más de una derivación para ella en una gramática.

Una gramática es ambigua si su lenguaje contiene una sentencia ambigua, es decir, se puede derivar la misma sentencia con dos (o más) derivaciones distintas.

Un lenguaje es ambiguo (o incluso se dice inherentemente ambiguo) si todas las gramáticas que generan el lenguaje son ambiguas.

Ejemplo: $G=(\{\$\},\{1\},\{\$\longrightarrow 11\},\$)$ no es ambigua, entonces $L(G)$ no es ambiguo.

Si una sentencia es ambigua (en el caso de las gramáticas libres de contexto) tenemos dos árboles de derivación para la misma sentencia.

Ejemplo:

$$E \longrightarrow E+E\;\vert\;E*E\;\vert\;(E)\;\vert\;a \;\vert\;\dots\;\vert\;z, \$\longrightarrow E$$

La ambigüedad introduce cierto grado de indeterminismo para derivar palabras, por eso, en la práctica se intenta evitar gramáticas ambiguas.

(Pero: el problema de decisión, si existe para una gramática ambigua una gramática equivalente no-ambigua es un problema no-computable.)

Investigamos de nuevo las expresiones aritméticas:

• sabemos que tanto la adición como la multuplicación son asociativas, entonces podemos acordar generar siempre con derivaciones más a la izquierda
• sabemos que hay prioridades (acordadas) entre las operaciones: $()$ antes que $*$ antes que $+$, entonces podemos acordar generar primero las operaciones con menos prioridad
• podemos introducir varables adicionales que nos garantizan una derivación única

Usamos $E$ para expresiones (va a ser también el símbolo inicial), $T$ para termios (con prioridad asociado a $+$), $F$ para factores (con prioridad asociado a $*$, y $V$ para variables (que ya no tendrán operaciones):

$$\begin{eqnarray*} E&\longrightarrow &E+T\;\vert\;T \\ T&\longrightarrow &T*F\;\... ...t\;V \\ V&\longrightarrow & a\;\vert\;b\;\vert\;\dots\;\vert\;z \end{eqnarray*}$$

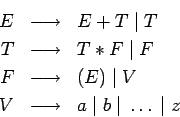
La gramática con este sistema de producciones no es ambigua.