



Siguiente: Equivalencia y ambigüedad
Subir: Gramáticas generativas
Anterior: Árbol de derivación
Índice General
Según Chomsky se clasifica las gramáticas en cuatro
tipos (cuales son, como vemos más adelante, entre si
verdaderamente diferentes).
Entonces sea
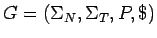 una gramática
(y
una gramática
(y
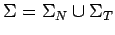 ). Las gramáticas se
destinguen solamente en el sistema de producciones que siempre será
un conjunto finito y que se clasifica en los siguientes tipos:
). Las gramáticas se
destinguen solamente en el sistema de producciones que siempre será
un conjunto finito y que se clasifica en los siguientes tipos:
- Tipo 0:
- gramáticas generales sin restricciones
es decir, se sustituye por lo menos un símbolo no-terminal.
- Tipo 1:
- gramáticas sensibles al contexto
es decir, se sustituye un símbolo no-terminal por algo manteniendo
el contexto; entonces una derivación siempre produce palabras más
largas o iguales (
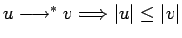 )
)
- Tipo 2:
- gramáticas libres de contexto
es decir, se sustituye solo símbolos no-terminales por palabras
no vacías
- Tipo 3:
- gramáticas regulares (o lineales)
es decir, lineales a la izquierda (porque los símbolos no-terminales
aparecen en una derivación siempre a la izquierda de la palabra)
es decir, lineales a la derecha (porque los símbolos no-terminales
aparecen en una derivación siempre a la derecha de la palabra)
- Se ha introducido explícitamente la regla
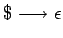 en
las gramáticas de tipos 1, 2, y 3 para permitir que el lenguaje
en
las gramáticas de tipos 1, 2, y 3 para permitir que el lenguaje
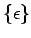 puede ser generado dado que las reglás solo permiten
un crecimiento de la longitud de las palabras a lo largo de las
derivaciones.
puede ser generado dado que las reglás solo permiten
un crecimiento de la longitud de las palabras a lo largo de las
derivaciones.
- Retomamos la clasificación de las gramáticas hacia final
del curso (por ejemplo, respondemos a la pregunta si son de verdad
clases separadas).
Observación: si permitimos para las gramáticas
de libre contexto reglas del tipo
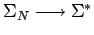 , es decir,
permitimos reglas como
, es decir,
permitimos reglas como
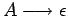 , podemos sustituir todas
las reglas que tengan una
, podemos sustituir todas
las reglas que tengan una 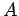 a la derecha, por ejemplo
a la derecha, por ejemplo
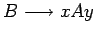 por
por
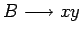 , y conseguir así una eliminación de las producciones
compresoras.
, y conseguir así una eliminación de las producciones
compresoras.




Siguiente: Equivalencia y ambigüedad
Subir: Gramáticas generativas
Anterior: Árbol de derivación
Índice General
© 2006, Dr. Arno Formella, Universidad de Vigo, Departamento de Informática
![]() una gramática
(y
una gramática
(y
![]() ). Las gramáticas se
destinguen solamente en el sistema de producciones que siempre será
un conjunto finito y que se clasifica en los siguientes tipos:
). Las gramáticas se
destinguen solamente en el sistema de producciones que siempre será
un conjunto finito y que se clasifica en los siguientes tipos:
![]() , es decir,
permitimos reglas como
, es decir,
permitimos reglas como
![]() , podemos sustituir todas
las reglas que tengan una
, podemos sustituir todas
las reglas que tengan una ![]() a la derecha, por ejemplo
a la derecha, por ejemplo
![]() por
por
![]() , y conseguir así una eliminación de las producciones
compresoras.
, y conseguir así una eliminación de las producciones
compresoras.