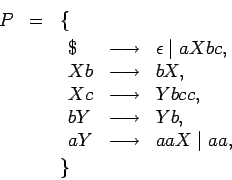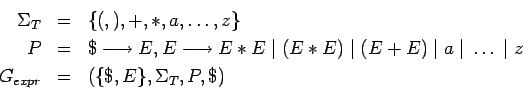Abreviación de Backus

Para abreviar la notación de las producciones usamos la forma normal de Backus (BNF). Agrupamos las producciones cuyas partes izquierdas coincidan, escribiendo las partes derechas separadas por 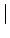$\vert$, por ejemplo:

$$\begin{eqnarray*} P &=&\{\\ && \begin{array}{lcl} \$ &\longrightarrow & \epsilo... ...\\ aY &\longrightarrow & aaX\;\vert\;aa,\\ \end{array}\\ &&\} \end{eqnarray*}$$

Definimos una gramática que genere lo que se usa en programas, por ejemplo:

$$((a+b)*(c+d))*(e+f)$$

$$\begin{eqnarray*} L_{expr}&=&\{w\;\vert\;w \mbox{ es expresi\'on algebraica}\} \end{eqnarray*}$$

donde nos limitamos a variables que consisten de una sola letra. Entonces

$$\begin{eqnarray*} \Sigma_T&=&\{(,),+,*,a,\dots,z\} \\ P &=& { \$\longrightarrow... ...;\vert\;\dots\;\vert\;z }\\ G_{expr}&=&(\{\$,E\},\Sigma_T,P,\$) \end{eqnarray*}$$

• se puede ampliar la gramática que incluye también 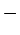$-$ y $/$
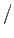
• se puede ampliar la gramática que genere también expresiones con variables de más de una letra, por ejemplo: $ancho*altura$
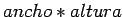
• más tarde veremos como se define las expresiones de tal estilo un poco más completo