



Siguiente: Abreviación de Backus
Subir: Gramáticas generativas
Anterior: Gramáticas generativas
Índice General
¿Es posible derivar lenguajes infinitos con sistemas de producciones
finitos?
Si, por ejemplo es posible generar el lenguaje
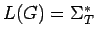 con
un sistema de producciones finitos:
con
un sistema de producciones finitos:
- obviamente
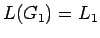
- para lenguajes finitos es fácil generar una gramática,
basta con derivar directamente cada palabra desde el símbolo
inicial (aunque se puede usar un sistema de producciones más
sofisticado)
Una gramática recursiva sobre la palabra
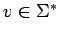 es una gramática donde se puede derivar desde
es una gramática donde se puede derivar desde 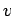 una palabra que contiene
una palabra que contiene
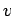 de nuevo, es decir, existe la posibilidad de una derivación:
de nuevo, es decir, existe la posibilidad de una derivación:
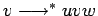 (con
(con 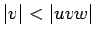 ).
).
El lenguaje generado por una gramática es infinito, si
la gramática es recursiva sobre una palabra 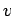 y que a su vez es derivable
desde el símbolo inicial.
y que a su vez es derivable
desde el símbolo inicial.
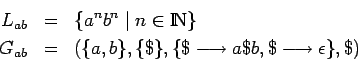
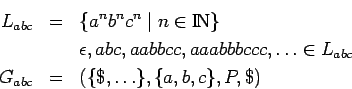
- ¿Cuáles son las producciones necesarias?
- Una vez sabiendo eso, podemos completar el alfabeto no-terminal
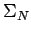
- Una primera idea:
Obviamente podemos derivar cualquier elemento de 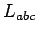 con esa
gramática, por ejemplo:
con esa
gramática, por ejemplo:
Pero también podemos derivar palabras como 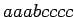 , es decir,
el lenguaje es
, es decir,
el lenguaje es
Parece que la gramática
 es demasiado amplia.
De alguna manera deberíamos construir un sistema de producciones
que permite mantener un número igual de letras
es demasiado amplia.
De alguna manera deberíamos construir un sistema de producciones
que permite mantener un número igual de letras 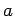 ,
, 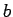 y
y 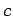 (o en otras palabras, necesitamos ``contar'')...
(o en otras palabras, necesitamos ``contar'')...
- Idea 1: Si somos capaz de derivar desde
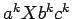 la secuencia
la secuencia
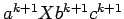 , hemos ganado.
, hemos ganado.
Idea 2: Tenemos que pasar la ``información'' que hemos añadido
por ejemplo un 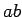 en un lado hacia el otro lado donde tenemos que
añadir entonces una
en un lado hacia el otro lado donde tenemos que
añadir entonces una 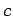 (o en un lado la
(o en un lado la 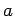 y en el otro lado un
y en el otro lado un 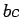 ).
).
El truco consiste en usar unos símbolos no-terminales cuales se
van a sustituir dependiendo del contexto en el cual se encuentran.
Entonces, construimos 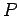 y
y 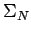 :
:
- Se puede comprobar formalmente con inducción sobre
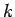 que la
gramática dada genera exactamente el lenguaje deseado,
es decir
que la
gramática dada genera exactamente el lenguaje deseado,
es decir
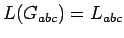 .
.
La comprobación sigue la construcción y se observa que
no hay ambigüedad en el momento de elegir una producción.
- Existe también una gramática que usa un símbolo no-terminal
menos y también una producción menos:
Se observa:
- tenemos ambigüedad en elegir producciones para sustituir y dónde
aplicarlas
- aquí hemos decidido añadir a la derecha una
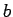 y una
y una 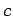
- generalmente se nota que hay muchas gramáticas que generan
el mismo lenguaje




Siguiente: Abreviación de Backus
Subir: Gramáticas generativas
Anterior: Gramáticas generativas
Índice General
© 2006, Dr. Arno Formella, Universidad de Vigo, Departamento de Informática
![]() con
un sistema de producciones finitos:
con
un sistema de producciones finitos:
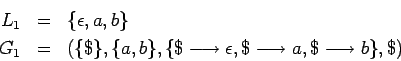
![]() es una gramática donde se puede derivar desde
es una gramática donde se puede derivar desde ![]() una palabra que contiene
una palabra que contiene
![]() de nuevo, es decir, existe la posibilidad de una derivación:
de nuevo, es decir, existe la posibilidad de una derivación:
![]() (con
(con ![]() ).
).
![]() y que a su vez es derivable
desde el símbolo inicial.
y que a su vez es derivable
desde el símbolo inicial.
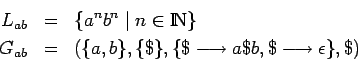
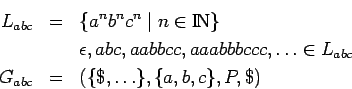
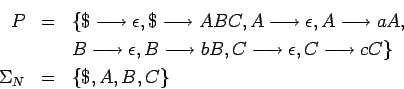
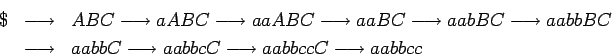
![]() en un lado hacia el otro lado donde tenemos que
añadir entonces una
en un lado hacia el otro lado donde tenemos que
añadir entonces una ![]() (o en un lado la
(o en un lado la ![]() y en el otro lado un
y en el otro lado un ![]() ).
).
![]() y
y ![]() :
:

