



Siguiente: Relación de equivalencia de
Subir: Conceptos básicos
Anterior: Producciones y Derivaciones
Índice General
Un conjunto
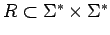 es una relación (binaria sobre
es una relación (binaria sobre
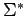 ).
).
Escribimos los pares siendo elementos de 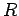 como
como 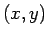 ,
o como
,
o como
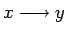 , o como
, o como 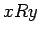 .
.
Sean 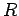 y
y 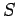 dos relaciones. Definimos
dos relaciones. Definimos
es decir, 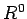 es la relación de identidad, y la operación nos permite
crear nuevas relaciones a partir de dos relaciones dadas, y
es la relación de identidad, y la operación nos permite
crear nuevas relaciones a partir de dos relaciones dadas, y 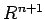 es una
relación construida de tal manera recursivamente. Con eso definimos:
es una
relación construida de tal manera recursivamente. Con eso definimos:
es decir, 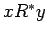 (o en otra notación
(o en otra notación
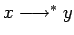 ) si
) si 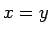 o
existe una secuencia
o
existe una secuencia
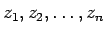 con
con 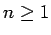 y
y
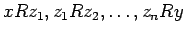 .
.
Una relación 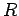 es
es
- reflexiva, si
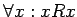 , es decir, la relación
de identidad
, es decir, la relación
de identidad 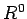 es subrelación de
es subrelación de 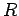 ,
,
- transitiva, si
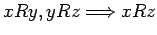 , es decir, si
los pares
, es decir, si
los pares 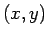 y
y 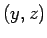 son elementos de
son elementos de 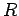 entonces
entonces 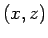 también lo es,
también lo es,
- simétrica, si
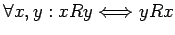 , es decir,
con
, es decir,
con 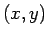 también
también 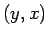 es elemento de la relación.
es elemento de la relación.
Observamos que para 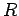
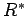 es una relación reflexiva y transitiva, llamada la
clausura reflexiva y transitiva de
es una relación reflexiva y transitiva, llamada la
clausura reflexiva y transitiva de 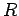 (porque es la relación más pequeña
con tal propiedad).
(porque es la relación más pequeña
con tal propiedad).
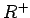 es una relación transitiva, llamada la
clausura transitiva de
es una relación transitiva, llamada la
clausura transitiva de 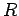 (porque es la relación más pequeña
con tal propiedad).
(porque es la relación más pequeña
con tal propiedad).
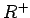 es también reflexiva si
es también reflexiva si 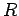 ya lo es.
ya lo es.
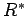 y
y 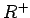 son simétricas si
son simétricas si 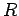 ya lo es.
ya lo es.
Una relacion 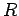 es una relación de equivalencia
si
es una relación de equivalencia
si 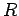 es reflexiva, simétrica, y transitiva.
es reflexiva, simétrica, y transitiva.
Sea 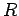 una relación de equivalencia. A cada elemento de
una relación de equivalencia. A cada elemento de
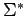 podemos asignar el conjunto de los elementos que son equivalentes a él.
Basta con anotar un representente de dicho conjunto y escribimos
podemos asignar el conjunto de los elementos que son equivalentes a él.
Basta con anotar un representente de dicho conjunto y escribimos
(si desde el contexto ya conocemos 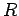 , obviamos del subindice
, obviamos del subindice 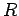 ).
).
Si 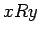 entonces
entonces ![$[x]=[y]$](img185.gif) porque ambos caen en la misma clase de
equivalencia. Se suele usar como representante una de las palabras más
cortas de la clase.
porque ambos caen en la misma clase de
equivalencia. Se suele usar como representante una de las palabras más
cortas de la clase.
Si ![$x,y\in[z]$](img186.gif) escribimos también
escribimos también 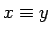 que significa que
que significa que
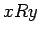 e
e 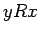 .
.
Una relación de equivalencia divide
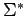 en clases, es decir,
en clases, es decir,
cuyo número es finito o infinito. La intersección de dos
clases es vacía, es decir,
![$[x_i]\cap[x_j]=\emptyset$](img190.gif) si
si 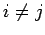 porque si tuviesen un elemento en común, ambas clases serían
iguales.
porque si tuviesen un elemento en común, ambas clases serían
iguales.
Ejemplo: Sea
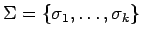 un
alfabeto (por ejemplo el alfabeto de toda la vida).
un
alfabeto (por ejemplo el alfabeto de toda la vida).
La relación
es una relación de equivalencia y nos divide
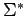 en
en
es decir, en todas las clases de palabras que empiezan con la misma
letra más la clase para la palabra vacía (que no empieza con ninguna
letra).
Entonces hay tantas clases como símbolos en 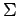 más una
clase.
más una
clase.
Llamamos el número de clases que produce una relación de equivalencia
el índice de la relación
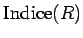 .
.
En el ejemplo tenemos
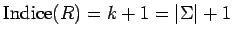 , es decir,
un índice finito.
, es decir,
un índice finito.




Siguiente: Relación de equivalencia de
Subir: Conceptos básicos
Anterior: Producciones y Derivaciones
Índice General
© 2006, Dr. Arno Formella, Universidad de Vigo, Departamento de Informática
![]() es una relación (binaria sobre
es una relación (binaria sobre
![]() ).
).
![]() como
como ![]() ,
o como
,
o como
![]() , o como
, o como ![]() .
.
![]() y
y ![]() dos relaciones. Definimos
dos relaciones. Definimos
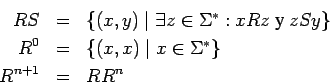
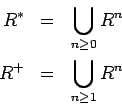
![]() es
es
![]()
![]() es una relación de equivalencia
si
es una relación de equivalencia
si ![]() es reflexiva, simétrica, y transitiva.
es reflexiva, simétrica, y transitiva.
![]() una relación de equivalencia. A cada elemento de
una relación de equivalencia. A cada elemento de
![]() podemos asignar el conjunto de los elementos que son equivalentes a él.
Basta con anotar un representente de dicho conjunto y escribimos
podemos asignar el conjunto de los elementos que son equivalentes a él.
Basta con anotar un representente de dicho conjunto y escribimos
![]() entonces
entonces ![]() porque ambos caen en la misma clase de
equivalencia. Se suele usar como representante una de las palabras más
cortas de la clase.
porque ambos caen en la misma clase de
equivalencia. Se suele usar como representante una de las palabras más
cortas de la clase.
![]() escribimos también
escribimos también ![]() que significa que
que significa que
![]() e
e ![]() .
.
![]() en clases, es decir,
en clases, es decir,
![]() un
alfabeto (por ejemplo el alfabeto de toda la vida).
un
alfabeto (por ejemplo el alfabeto de toda la vida).
![]() más una
clase.
más una
clase.
![]() .
.
![]() , es decir,
un índice finito.
, es decir,
un índice finito.