Clipping von Geradensegmenten

Betrachten drei Clipping-Algorithmen:

• Algorithmus nach clipcsCohen-Sutherland
• Algorithmus nach cliplbLiang-Barsky
• Algorithmus nach clipnlnNicholl-Lee-Nicholl

Algorithmus nach Cohen-Sutherland

clipcsIdee:

• Klassifizierung der Endpunkte bzgl. des Fensters
  • O oberhalb
  • U unterhalb
  • L links
  • R rechts
  mit jeweils einem Bit.
  Es entsteht ein Vier-Bit-Codewort
• Liegen beide Endpunkte auf der gleichen Seite des Fenster,
  dann kann man das ganze Segment verwerfen.
• Ist kein Bit gesetzt,
  dann liegt es vollständig im Innern des Fensters.
• Ansonsten schneidet man bzgl. eines Randes des Fensters ab und verfährt analog mit dem abgeschnittenen Segement.

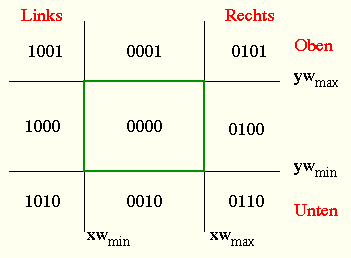
Formulieren wir einige benötigte einfache Funktionen:

int Encode(point p)

Liefert Codewort für einen Punkt zurück

int Encode(point p) {
  return
      ( ( ( ( ( (p.x > y_max)
                << 1
              ) | (p.x < y_min)
            ) << 1
          ) | (p.x < x_min)
        ) << 1
      ) | (p.x > x_max);
}

wobei x_min, x_max, y_min, und y_max die Fensterkoordinaten sind.

int Inside(int code_p)

Ein Punkt liegt innerhalb, wenn kein Bit im Codewort gesetzt ist, also return(!code_p).

int Accept(int code_p, int code_q)

Ein Segment wird akzeptiert, wenn in keinem der beiden Codeworte ein Bit gesetzt ist, also return(code_p|code_q).

int Reject(int code_p, int code_q)

Ein Segment wird verworfen, wenn in beiden Codeworten ein Bit an der gleichen Stelle gesetzt ist, also return(code_p&code_q).

point Intersect(point p, point q, int border)

Liefert Schnittpunkt der Segmentes mit der entsprechenden Geraden des Fensters (Übung!).

void Swap(..., ...)

Vertauscht die beiden Argumente (Übung!).

Algorithmus:
(als C++-Programmgerüst, welches das Segment zeichnet und leicht als Übung vervollständigt werden kann.)

 
void ClipCohenSutherland(
  point p, point q
) {
  enum State { NOTDONE, ACCEPT, REJECT };
  State done(NOTDONE);

  while(done != ACCEPT && done != REJECT ) {
    code_p = Encode(p);
    code_q = Encode(q);
    if ( Accept(code_p,code_q) ) done = ACCEPT;
    else {
      if ( Reject(code_p,code_q) ) done = REJECT;
      else {
        if ( Inside(code_p) ) {
          Swap(&p,&q);
          Swap(&code_p,&code_q);
        }
        if (code_p&LEFT) {
          p = Intersect(p,q,left_border);
        else if (code_p&RIGHT) {
          p = Intersect(p,q,right_border);
        }
        else ...
      }
    }
  }
  if (done == ACCEPT) DrawLine(p,q,color);
}

Algorithmus nach Liang-Barsky

cliplbIdee:

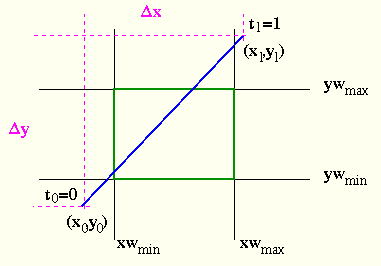
Betrachten parametrisierte Form des Segmentes

$$\begin{eqnarray*} \Delta x &=& x_1-x_0 \\ \Delta y &=& y_1-y_0 \\ &&\\ x &=& x_0+t\Delta x \\ y &=& y_0+t\Delta y \qquad 0\leq t\leq 1\\ \end{eqnarray*}$$

Dieses muss innerhalb des Fensters liegen. Wir erhalten also die Bedingungen:

$$xw_{\min}\leq x_0+t\Delta x \leq xw_{\max}$$

$$yw_{\min}\leq y_0+t\Delta y \leq yw_{\max}$$

Dies sind vier Ungleichungen der Form:

$$t\cdot p_k \leq q_k\qquad k=1,2,3,4$$

Nämlich

$$\begin{eqnarray*} t\cdot(-\Delta x) &\leq& x_0-xw_{\min} \\ t\cdot\Delta x &\le... ... y) &\leq& y_0-yw_{\min} \\ t\cdot\Delta y &\leq& yw_{\max}-y_0 \end{eqnarray*}$$

Bemerkung: die Ausdrücke für $p_k$ und $q_k$ ergeben sich auch aus der secintersectSchnittpunktberechnung zwischen Segmenten, wenn man berückschtigt, dass die Fensterbegrenzungen horizontal bzw. vertikal verlaufen und damit in den Determinanten Nullen auftauchen.

Idee des Verfahrens:

• wir betrachten orientierte Gerade durch das Segment mit Ursprung in einem der Endpunkte
• da die Segmentgerade orientiert ist, kann man entscheiden, ob man von Innen nach Außen oder umgekehrt von Außen nach Innen eine Fenstergerade schneidet
• wir berechnen die Parameterwerte der bis zu vier Schnittpunkte. (Sofern die Gerade nicht parallel zu einer der Fenstergeraden ist; siehe letzten Punkt)
• wir berechnen das Minimum der Parameterwerte für ``von Innen'' und 0
• wir berechnen das Maximum der Parameterwerte für ``von Außen'' und 1
• ist das Minimum kleiner als das Maximum, so liegt das dazwischenliegende Geradensegment im Fenster
• liegt die Gerade parallel zu einer Fenstergerade, so kann man anhand von $q$ entscheiden, ob das Segment außerhalb liegt

Sofern die Differenz für $p_k$ nicht Null ist, können wir $t$ jeweils durch eine Division berechnen:

$$t=q_k/p_k$$

Ist ein $p_k=0$, so verläuft das Segment parallel zu einer der Fensterseiten, ist dann $q_k<0$, so liegt es auserhalb.

Ist ein $p_k<0$, so läuft man bzgl. der parametrisierten Gleichung von Außen nach Innen, also verschieben wir $t_0$.

Ist ein $p_k>0$, so läuft man bzgl. der parametrisierten Gleichung von Innen nach ßen, also verschieben wir $t_1$.

Es muss natürlich stets gelten: $t_0<t_1$, da wir uns entlang des Segmentes bewegen.

Algorithmus:
(als C++-Programmgerüst, welches zeichnet und leicht als Übung vervollständigt/modifiziert werden kann.)

Die Funktion ClipTest() testet jeweils für eine der Ungleichungen, d.h. Fensterbegrenzung, und aktualisiert gegebenenfalls die Parameter:

 
bool ClipTest(
  double p, double q,
  double& t0, double& t1
) {
  if( p < 0 ) {
    double t(q/p);
    if( t > t1 ) return false;
    t0 = Max(t0,t);
  }
  else if( p > 0 ) {
    double t(q/p);
    if( t < t0 ) return false;
    t1 = Min(t1,t);
  }
  else if( q < 0 ) return false;
  return true;
}

Hauptfunktion:

 
void ClipLiangBarsky(
  point P, point Q
) {
  double t0(0.0);
  double t1(1.0);

  double Dx(q.x-p.x);
  if( ClipTest(-Dx, P.x-xwmin, t0, t1) ) {
    if( ClipTest(Dx, xwmax-P.x, t0, t1) ) {
      double Dy(Q.y-P.y);
      if( ClipTest(-Dy, P.y-ywmin, t0, t1) ) {
        if( ClipTest(Dy, ywmax-P.y, t0, t1) ) {
          if( t0 > 0 ) {
            P.x = P.x + t0*Dx;
            P.y = P.y + t0*Dy;
          }
          if( t1 < 1) {
            Q.x = P.x + t1*Dx;
            Q.y = P.y + t1*Dy;
          }
          DrawLine(P,Q,color);
        }
      }
    }
  }
}

Liang-Barsky Clipping kommt mit einer Division pro Fensterseite als arithmetischer Operation aus, womit er u.U. effizienter als der Cohen-Sutherland-Algorithmus zu implementieren ist. Auch kommen im Mittel weniger Schnittpunktberechnungen mit den Fensterbegrenzungen vor (hier sind die Aussagen in der Literatur aber uneinheitlich).

Algorithmus von Nicholl-Lee-Nicholl

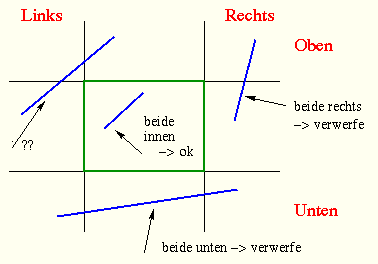
clipnlnHier werden die eventuell unnötigen Schnittpunktberechnungen der anderen Algorithmen eliminiert, indem das Gebiet in weitere Regionen unterteilt wird, in denen sich die Endpunkte befinden können. Damit erreicht man, dass nur genau mit den Fensterbegrenzungen ein Schnittpunkt berechnet wird, wo wirklich ein Schnittpunkt mit dem Fenster auftritt.

(Tafelerklärung, wird noch ergänzt)

Der NLN-Algorithmus ist nicht leicht auf 3 Dimensionen zu erweitern, was ein Vorteil der anderen beiden Verfahren ist (wir sehen es wieder wenn wir rayboxinterStrahl-Box-Schnittpunkte im RayTracing-Algorithmus untersuchen). NLN kommt im Mittel aber mit weniger arithmetischen Operationen aus.

Beachte: Heute sollte man jedoch weniger die Anzahl der arithmetischen Operationen vergleichen, als vielmehr die Möglichkeiten einer parallelen oder gepipelineten Ausführung der Operationen, sowie die Sprungstruktur zwischen den Basisblöcken des Programmcodes (viele ifs sind u.U. weniger effizient als einige Divisionen).

Folgende Tabelle zeigt einige Laufzeitmessungen und auch einen Vergleich mit einer geschickten Implementierung des Clippings, welche Festkommazahlen benutzt und weitere Optimierungen verwendet (der Artikel spezifiziert den tatsächlichen Algorithmus allerdings nicht ?!)

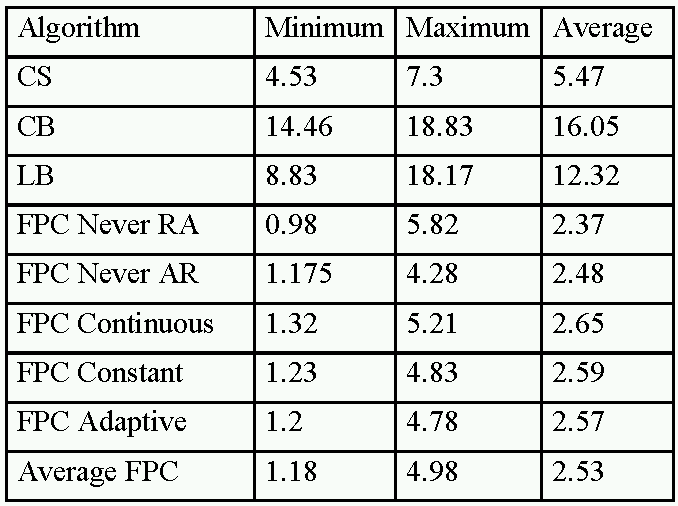
LB steht für Liang-Barsky, CS für Cohen-Sutherland, FPC für die neue? Methode in verschiedenen Variationen (siehe Originalartikel).

Interessant wäre z.B. eine MMX/SSE-Implementierung oder was immer die CPU/GPU zur Verfügung stellt, bei der man alle $t$-Werte für die Schnittpunkte mit den vier Fensterbegrenzungen parallel berechnet und dann anschließend geschickt auswählt und berechnet.