



Nächste Seite: Diskretisierung der parametrisierten Form
Aufwärts: Darstellung von Ellipsen
Vorherige Seite: Mögliche Beschreibungsformen für eine
Inhalt
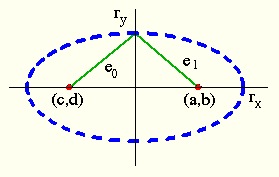
Mit 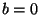 ,
, 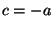 , und
, und 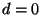 und wegen
und wegen
ergibt sich
Und man kann 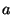 angeben als
angeben als
und alles in die implizite Gleichung einsetzen:
Diese Gleichung vereinfacht man leicht (mit Maple!) zu:
oder auch in anderer Form
Damit erhalten wie die implizite Form zu:
Und eine Verschiebung liefert:
Als Aufrufparameter zum Zeichnen einer achsenparallelen Ellipse
haben wir also:
DrawEllipse(x0,y0,rx,ry,color)
© 2004/2005, A. Formella & D. Fellner, Universität Braunschweig


![]() ,
, ![]() , und
, und ![]() und wegen
und wegen
![]() angeben als
angeben als