Mögliche Beschreibungsformen für eine Ellipse

implizite Form:

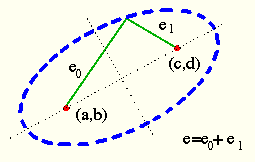
Gegeben: die beiden Fokuspunkte $(a,b)$ und $(c,d)$ sowie die Fokusdistanz $e$:

$$\begin{eqnarray*} F(x,y) &=& 0 \\ & & \\ F(x,y) &=& \sqrt{(x-a)^2+(y-b)^2}+\sqrt{(x-c)^2+(y-d)^2}-e \quad \mbox{und}\quad (c-a)^2+(d-b)^2<e^2 \end{eqnarray*}$$

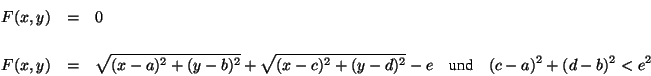
und es gilt:

$$\begin{eqnarray*} F(x,y) && \left\{\begin{array}{ll} < 0 & \quad\mbox{innerhal... ... > 0 & \quad\mbox{au{\ss}erhalb der Ellipse} \end{array}\right. \end{eqnarray*}$$

explizite Form:

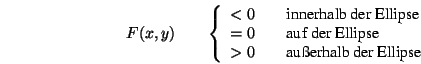
welche ``etwas'' komplex ist, am Besten man verwendet ein Algebrasystem (z.B. Maple Waterloo Maple Inc.), um die explizite Form aus der impliziten Form zu bestimmen:

$$\begin{eqnarray*} y &=& f(x) \\ & & \\ \lefteqn{f(x) = 1/(2\cdot(-4e^2+4d^2+4... ...\right] \\ & & \\ & & \mbox{und}\quad \sqrt{(c-a)^2+(d-b)^2}<e \end{eqnarray*}$$

parametrisierte Form:

siehe zweidimensionale Transformationen