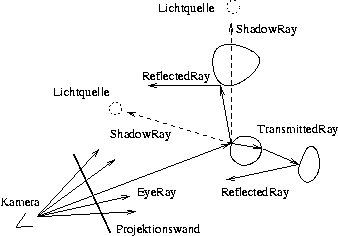
Da es nicht praktikabel ist, alle von einem strahlenden Objekt ausgesendeten Strahlen zu verfolgen, geht man den umgekehrten Weg. Die potentiell ins Auge einfallenden Lichtstrahlen werden zurückverfolgt. Ein Schnitt im entstehenden Strahlkegel wird als Projektionsfläche dargestellt. Treffen die Strahlen auf Oberflächen, werden sie entsprechend den optischen Gesetzen (Reflexion, Transparenz, Brechung usw.) gespiegelt bzw. gebrochen. Die Strahlen transportieren die Energie (Farbe und Intensität, je nach Farbmodell RGB, YIQ (YUV), HSL usw.) des Lichtes.
Die von einer Lichtquelle ausgesendete Energie wird so für den in das Auge einfallenden Strahl berechnet.
Obige Abbildung veranschaulicht die Vorgehensweise. Im Folgenden wird auf die dort gemachten Bezeichnungen für die verschiedenen Strahlen zurückgegriffen. Der Algorithmus arbeitet also wie folgt:
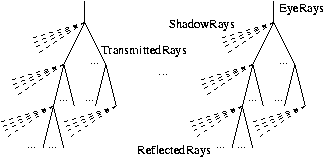
Ändert sich die Kameraposition, d.h. der Punkt von dem aus die Kamerastrahlen erzeugt werden, oder bewegt sich ein Objekt, dann müssen eventuell große Teile der Strahlbäume neu aufgebaut werden.
Als Anzahl der Strahlen, die bei der Berechnung eines Bildes anfallen,
erhält man also:
Für jeden dieser Strahlen muss der Schnittpunkttest durchgeführt werden.
Implementiert man dies auf sehr naive Art und Weise, erfordert dies z.B. ein lineares Suchen über alle Objekte. Die Zeit zur Berechnung eines
Schnittpunktes bezeichnen wir im folgenden mit 
. Will man weiterhin
nicht nur ein Einzelbild, sondern eine ganze Sequenz von Bildern erzeugen,
vervielfacht sich der Aufwand mit der Länge der Sequenz 
.
Die Laufzeit beträgt somit (in Einheiten eines Schnittpunkttests) ohne
Berücksichtigung der Berechnungen des Beleuchtungsmodells und anderer
Vorbereitungs- und Nachbereitungszeiten:
,
,
erhält man:
