Unser Ziel ist es eine einfache Billard-Animation zu programmieren.
Annahme: Kugeln bewegen sich zwischen zwei Kollisionen mit konstanter, ungedämpfter Geschwindigkeit auf geradliniger Bahn.
Zwei Kugeln treffen sich, wenn sie gerade soweit zusammen kommen, dass der Abstand der beiden Mittelpunkte gleich der Summe der Radien ist.
Gegeben:
| Ausgangszeitpunkt | |
| Position Kugel 0 zum Ausgangszeitpunkt | |
| Geschwindigkeit Kugel 0 | |
| Radius Kugel 0 | |
| Position Kugel 1 zum Ausgangszeitpunkt | |
| Geschwindigkeit Kugel 1 | |
| Radius Kugel 1 |
Bewegungsgleichungen (sind Vektorgleichungen):
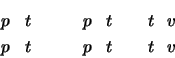
z.B. im 2-Dimensionalen für die erste Gleichung:
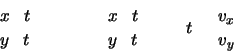
Kollisionsbedingungen:
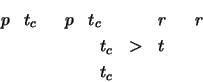
d.h. Zeitpunkt ![]() liegt in der Zukunft und ist der erste Zeitpunkt,
an dem sich beide Kugeln gerade berühren.
liegt in der Zukunft und ist der erste Zeitpunkt,
an dem sich beide Kugeln gerade berühren.
Wir kennen Zusammenhang zwischen Betrag und Skalarprodukt:
Einsetzen:
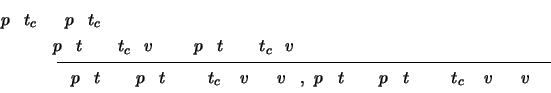
Verwenden:
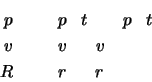
Lösen:

Verwenden:
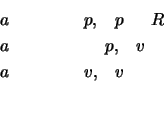
Also Lösen der quadratischen Gleichung
liefert bei existierender minimaler Lösung größer ![]() den
Kollisionszeitpunkt.
den
Kollisionszeitpunkt.
Schreiben wir das Skalarprodukt mit einem einfachen Punkt statt
mit der Klammernotation, erhalten wir die quadratische Gleichung
in ![]() :
: