next_inactive up previous


Teoría de la Información: Modelado y Análisis

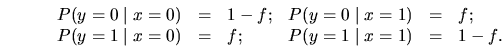
Arno Formella

Curso

La página incial del curso es:

http://formella.webs.uvigo.es/doc/tc03

Estos apuntes se acompaņa con ilustraciones en pizarra dónde se explica las notaciones y algunos de los conceptos.

El texto es meramente una brevísima introducción (5 horas) a la teoría de la información.

Bibliografía

Libros:
 

Tareas para una Presentación

digital fountain codes:
 
cuckoo hashing:
 
advanced information visualization:
 

Motivación

¿Qué es información?

una opinión:

es decir, la información depende del estado de ambas partes.

intercambio de información con mutuo acuerdo, es decir, fuente y destino han acordado un protocolo para interpretar los símbolos intercambiados entre ellos

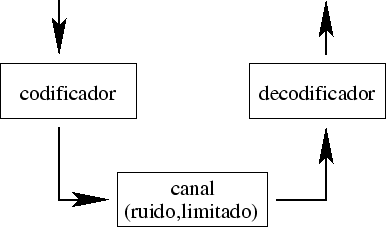
el canal de comunicación puede ser no-perfecto (p.ej., modem--línea telefónica--modem, satélite--propagación--tierra, memoria--disco--memoria)

la transmisión no se puede ver solamente en el sentido de espacio, sino también en el tiempo

si no hay protocolo establecido entre fuente y destino, el destino puede intentar averiguar el proceso de la fuente como manda la información

la teoría de información se dedica a los problemas de:

canal binario simétrico:


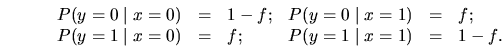
\begin{displaymath} \begin{array}{ccl}%%%%%% {c@{}c@{}l} %%%%% (for twocolumn st... ...x=1) &= & {f}; \\ P(y=1 \;\vert\;x=1) &= & 1 - {f}. \end{array}\end{displaymath}

\includegraphics[width=15cm]{bisymchn.eps}

\includegraphics{canal.eps}

Ejemplo: disco duro

asumimos canal binario simétrico para leer y escribir los bits al disco con una probabilidad de fallo de 0.1%

para que el disco sea útil, necesitamos una probabilidad de $10^{-15}$ intercambiando 1 GByte cada día durante 10 años.

códigos de repetición

usamos para cada bit tres bits y decidimos por voto mayoritario


\begin{displaymath} \begin{array}{rccccccc} {\mathbf s}& {\tt0}&{\tt0}&{\tt 1}... ... \mbox{fallos no corregidos} & & & & &\star & & \end{array}\end{displaymath}

\includegraphics[width=\textwidth]{repet.eps}

(7,4)-Hamming códigos

se manda en vez de 4 bits 7 bits

codificación:

${\mathbf s}$ ${\mathbf t}$
0000 0000000
0001 0001011
0010 0010111
0011 0011100
   
${\mathbf s}$ ${\mathbf t}$
0100 0100110
0101 0101101
0110 0110001
0111 0111010
   
${\mathbf s}$ ${\mathbf t}$
1000 1000101
1001 1001110
1010 1010010
1011 1011001
   
${\mathbf s}$ ${\mathbf t}$
1100 1100011
1101 1101000
1110 1110100
1111 1111111
   

se observa: cada pareja se distingue por lo menos en 3 bits

¿Cómo se ha construido la table?

se puede describir la construcción del código también con una multiplicación con una matriz:


\begin{displaymath} {\mathbf t}= {\left[ \begin{array}{cccc} \tt 1 &\tt0 &\tt0 ... ... 1 &\tt0 &\tt 1 &\tt 1 \end{array} \right] } \cdot {\mathbf s} \end{displaymath}

descodificación:

se podría buscar la palabra que menos se destingue de la palabra transmitida (según su distancia Hamming)

o mejor

se calcula el síndrome que es el vector de bits que indica donde se ha violado la paridad

síndrome ${\mathbf z}$ 000 001 010 011 100 101 110 111
cambia nada $r_7$ $r_6$ $r_4$ $r_5$ $r_1$ $r_2$ $r_3$

el proceso de codificación solamente funciona adecuadamente si se asume que se ha cambiado un solo bit durante la transmisión

también se puede expresar el cálculo del síndrome con una multiplicación con una matriz:


\begin{displaymath} {\mathbf z}= \left[ \begin{array}{ccccccc} \tt 1&\tt 1&\tt ... ...1&\tt 1&\tt0&\tt0&\tt 1 \end{array} \right] \cdot {\mathbf r} \end{displaymath}

diagrama que relaciona tasa de transmisión con probabilidad de fallo

\includegraphics[width=\textwidth]{rateprop.eps}

\includegraphics[width=\textwidth]{hamming.eps}

Teorema (Shannon):

La tasa máxima (=capacidad) de un canal binario simétrico que permite la transmisión con error arbitrariamente pequeño se calcula como


\begin{displaymath} C(f) = 1 - H_2(f) = 1 - \left[ f \log_2 \frac{1}{f} + (1-f) \log_2 \frac{1}{1-f} \right] \end{displaymath}


\begin{picture}(1500,900)(0,0) \font\gnuplot=cmr10 at 10pt \gnuplot \sbox{\plotp... ...0pt}{0.736pt}} \put(799.0,83.0){\rule[-0.200pt]{3.373pt}{0.400pt}} \end{picture}

entonces, con el código apropriado basta con 2 discos duros (que sean lo suficientemente grande para almacenar un bloque) para garantizar una probabilidad de error tan pequeña como se desea, si la probabilidad de fallo en un bit es 0.1

Nociones básicas

Notaciones:

$\mbox{$\cal A$}=\{a_0,a_1,\ldots,a_{I-1}\}$ alfabeto con $I$ símbolos
$\mbox{$\cal P$}=\{p_0,p_1,\ldots,p_{I-1}\}$ distribución de probabilidades discretas
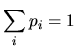  con $\displaystyle\sum_i p_i=1$ y $p_i\geq 0$
$x$ salida (o valor) de una variable aleatoria
$X=(x,\mbox{$\cal A$}_X,\mbox{$\cal P$}_X)$ ensemble, si $x\in \mbox{$\cal A$}_X$, $P(x=a_i)=p_i$

entonces:

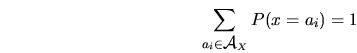
\begin{displaymath}\sum_{a_i\in \mbox{$\cal A$}_X}P(x=a_i)=1 \end{displaymath}

abbreviación: $P(x=a_i)=P(x)=P(a_i)$ dependiendo del contexto

Ejemplo:

$i$ $a_i$ $p_i$
1 a 0.0575
2 b 0.0128
3 c 0.0263
4 d 0.0285
5 e 0.0913
6 f 0.0173
7 g 0.0133
8 h 0.0313
9 i 0.0599
10 j 0.0006
11 k 0.0084
12 l 0.0335
13 m 0.0235
14 n 0.0596
15 o 0.0689
16 p 0.0192
17 q 0.0008
18 r 0.0508
19 s 0.0567
20 t 0.0706
21 u 0.0334
22 v 0.0069
23 w 0.0119
24 x 0.0073
25 y 0.0164
26 z 0.0007
27 - 0.1928


\begin{picture}(2,28)(-28,0) \put(-28,0.15){\makebox(0,0)[bl]{ % includegraphics... ...0.19 % put(-28.65,1 )\{ makebox(0,0)[r]\{\{ verb+-+\}\}\} % 0.19 \end{picture}

Notaciones:

$P(T)$ probabilidad de un subconjunto $T\subset \mbox{$\cal A$}_X$
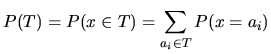  $P(T)=P(x\in T)=\displaystyle\sum_{a_i\in T}P(x=a_i)$
$XY$ ensemble unido
$(x,y)$ salida (o valor) de una variable aleatoria de un ensemble unido
  $x\in \mbox{$\cal A$}_X$ y $y\in \mbox{$\cal A$}_Y$
  las dos variables no son necesariamente independiente
$P(x,y)$ probabilidad unida
  $P(x,y)=P(x=a_i,y=b_i)$

dado un ensemble unido:

Vocabulario:

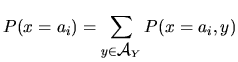probabilidad marginal $P(x=a_i)=\displaystyle\sum_{y\in \mbox{$\cal A$}_Y}P(x=a_i,y)$
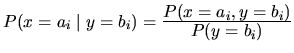probabilidad condicional $P(x=a_i\;\vert\;y=b_i)=\frac{\displaystyle P(x=a_i,y=b_i)}{\displaystyle P(y=b_i)}$
  si $P(y=b_i)\neq 0$
  probabilidad que $x$ sea $a_i$ dado que $y$ es $b_i$

Ejemplo:

\includegraphics[width=\textwidth]{joint.eps}

Reglas de cálculo

$\mbox{$\cal H$}$ denota bajo que condición se asume las probabilidades

Regla de producto (o regla de cadena):


\begin{displaymath} P(x,y \;\vert\;\mbox{$\cal H$}) = P(x \;\vert\;y , \mbox{$\c... ...y \;\vert\;x , \mbox{$\cal H$}) P( x \;\vert\;\mbox{$\cal H$}) \end{displaymath}

Regla de suma:

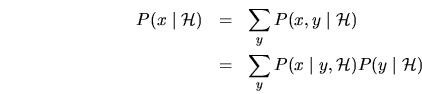
\begin{eqnarray*} P(x \;\vert\;\mbox{$\cal H$}) & = & \sum_y P(x,y \;\vert\;\mb... ...P(x \;\vert\;y , \mbox{$\cal H$}) P( y \;\vert\;\mbox{$\cal H$}) \end{eqnarray*}



Regla de BAYES:

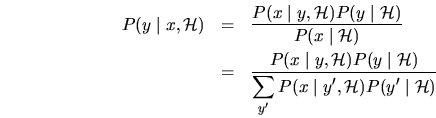
\begin{eqnarray*} P(y \;\vert\;x, \mbox{$\cal H$}) &=& \frac{ P(x \;\vert\;y , \... ...\;\vert\;y' , \mbox{$\cal H$}) P( y' \;\vert\;\mbox{$\cal H$}) } \end{eqnarray*}



Vocabulario:

independencia dos variables aleatorias $x$ e $y$ son independientes si:
  $P(x,y)=P(x)P(y)$

Ejemplo:

Solución:


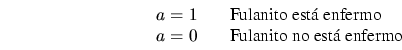
\begin{displaymath} \begin{array}{ccl} a=1 && \mbox{Fulanito est\'a enfermo} \\ a=0 && \mbox{Fulanito no est\'a enfermo} \end{array}\end{displaymath}


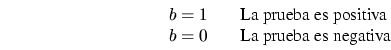
\begin{displaymath} \begin{array}{ccl} b=1 && \mbox{La prueba es positiva} \\ b=0 && \mbox{La prueba es negativa} \end{array}\end{displaymath}

probabilidades condicionales:


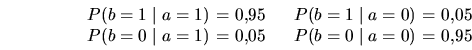
\begin{displaymath} \begin{array}{r@{\,\,=\,\,}l@{\ \ \:\:\:\:\:}r@{\,\,=\,\,}l}... ...ert\;a=1) & 0.05 & P(b=0 \;\vert\;a=0) & 0.95 \\ \end{array}\end{displaymath}

probabilidades marginales (de $a$):


\begin{displaymath} \begin{array}{c@{\,\,=\,\,}c@{\ \ \:\:\:\:\:}c@{\,\,=\,\,}c} P(a=1) & 0.01 & P(a=0) & 0.99 \\ \end{array}\end{displaymath}

probabilidad marginal (de $b=1$);


\begin{displaymath} P(b=1) = P(b=1 \;\vert\;a=1) P(a=1) + P(b=1 \;\vert\;a=0) P(a=0) \end{displaymath}

probabilidad que Fulanito esté enfermo:

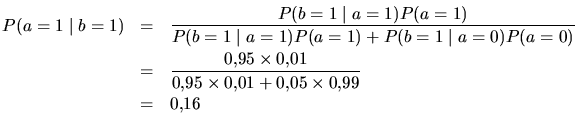
\begin{eqnarray*} P(a=1 \;\vert\;b=1) &=& \frac{ P(b=1 \;\vert\;a=1) P(a=1) } {... ...times 0.01 }{ 0.95 \times 0.01 + 0.05 \times 0.99 }\\ &=& 0.16 \end{eqnarray*}



es decir: solamente un 16%

si $P(a=1)=0.001$ la probabilidad baja a un 1.87%

Recomiendo leer la sección 2.3 del libro.

Notaciones:

$h(x)$ contenido de información de una salida $x$ (dado un ensemble)
  $h(x)=\log_2\frac{\displaystyle 1}{\displaystyle P(x)}$
$H(X)$ entropía de un ensemble
  es el contenido de información medio de una salida de un ensemble
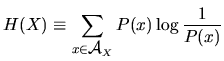  $H(X) \equiv \displaystyle\sum_{x \in \mbox{$\cal A$}_X} P(x) \log \frac{1}{P(x)}$

$i$ $a_i$ $p_i$ $h(p_i)$
1 a .0575 4.1
2 b .0128 6.3
3 c .0263 5.2
4 d .0285 5.1
5 e .0913 3.5
6 f .0173 5.9
7 g .0133 6.2
8 h .0313 5.0
9 i .0599 4.1
10 j .0006 10.7
11 k .0084 6.9
12 l .0335 4.9
13 m .0235 5.4
14 n .0596 4.1
15 o .0689 3.9
16 p .0192 5.7
17 q .0008 10.3
18 r .0508 4.3
19 s .0567 4.1
20 t .0706 3.8
21 u .0334 4.9
22 v .0069 7.2
23 w .0119 6.4
24 x .0073 7.1
25 y .0164 5.9
26 z .0007 10.4
27 - .1928 2.4
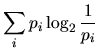$\displaystyle \sum_i p_i \log_2 \frac{1}{p_i}$ 4.1

Reglas para la entropía:

positivo:


\begin{displaymath} H(X) \geq 0 \end{displaymath}


\begin{displaymath} H(X) = 0 \qquad\Longleftrightarrow\qquad p_i=1 \mbox{\quad para un $i$} \end{displaymath}

confinado:


\begin{displaymath} H(X) \leq \log(\vert\mbox{$\cal A$}_X\vert) \end{displaymath}


\begin{displaymath} H(X)=\log(\vert\mbox{$\cal A$}_X\vert) \qquad\Longleftrightarrow\qquad \forall i: p_i = 1/\vert X\vert \end{displaymath}

ensembles unidos $X$ e $Y$:


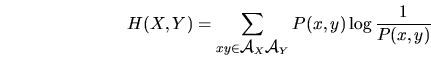
\begin{displaymath} H(X,Y) = \sum_{xy \in \mbox{$\cal A$}_X\mbox{$\cal A$}_Y} P(x,y) \log \frac{1}{P(x,y)} \end{displaymath}


\begin{displaymath} P(x,y)=P(x)P(y) \qquad\Longrightarrow\qquad H(X,Y) = H(X) +H(Y) \end{displaymath}

recursividad simple:


\begin{displaymath} H({\mathbf p}) = H( p_1 , 1\!-\!p_1 ) + (1\!-\!p_1) H \!... ...frac{p_3}{1\!-\!p_1} , \ldots , \frac{p_I}{1\!-\!p_1} \right) \end{displaymath}

recursividad general:

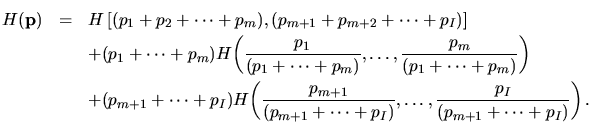
\begin{eqnarray*} H({\mathbf p}) &=& H\left[ ( p_1+p_2+\cdots+p_m ) , ( p_{m+1... ... ) } , \ldots , \frac{p_I}{ ( p_{m+1}+\cdots+p_I ) } \right) . \end{eqnarray*}



entropía relativa (o KULLBACK-LEIBLER divergencia)


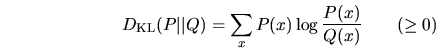
\begin{displaymath} D_{\mathrm{KL}}(P\vert\vert Q) = \sum_x P(x) \log \frac{P(x)}{Q(x)} \qquad(\geq 0) \end{displaymath}

siendo $P(x)$ y $Q(x)$ dos distribuciones de probabilidades sobre el mismo alfabeto

Compresión

compresión de datos, modelado de datos, y eliminación de ruído tienen mucho en común

¿Cómo se puede medir información?

Ejemplo con las 12 bolas...

según SHANNON medimos el contenido de información de un símbolo emitido por una fuente, con el logaritmo de base 2 de su probabilidad de aparencia.

¿Porqué el logaritmo?

porque para variables aleatorias independientes, es decir, con $P(x,y)=P(x)P(y)$ tenemos:

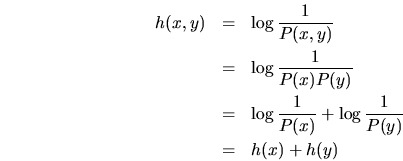
\begin{eqnarray*} h(x,y)&=&\log \frac{1}{P(x,y)} \\ &=&\log \frac{1}{P(x)P(y)... ... &=&\log \frac{1}{P(x)} + \log \frac{1}{P(y)} \\ &=& h(x)+h(y) \end{eqnarray*}



es decir, justamente sumamos sus contenidos de información individuales para obtener la información si ambos eventos ocurren a la vez.

el valor obtenido se puede interpretar como el número de bits necesarios para codificar la información.

¿Cuántos bits de información están escondidos en el ejemplo con las bolas?

¿Cuántos bits de información se gana con un uso de la báscula?

¿Qué propriedad tiene una solución óptima?

en cada uso de la báscula hay que intentar equilibrar las probabilidades de todos los posibles salidas del experimento.

por ejemplo, 6 contra 6 bolas núnca puede dar el caso de equilibrio.

\includegraphics[width=15cm]{bolas.eps}

¿Hay otra estrategia?

la comprobación del teorema de SHANNON trata también del caso que las probabilidades no son uniformes.

siguimos directamente con el libro ...

next_inactive up previous
© 2003, Dr. Arno Formella, Universidad de Vigo, Departamento de Informática