Editar imágenes

aplicamos las ondículas (principalmente las ondículas de Haar) para editar/pintar imágenes

en el campo de pintar imágenes se distingue normalemente entre dos tipos de imágines

• imágenes basadas en un mapa de píxeles, cuyo tamaño se suele fijar antes de empezar
• imágenes basadas en objectos, p.ej, líneas o otras primitivas geométricas

cualquier cambio de resolución de imágenes basadas en un mapa de píxeles necesita un proceso de filtrado y/o interpolación, para evitar la aparencia de bloques grandes o efectos de ``aliasing''

cambiar la resolución de imágenes basadas en objetos resulta más fácil porque se puede trasladar la operación al objeto, sin embargo, es muy difícil conseguir un cambio apropriado de propriedades que no sean basadas en una descripción unidimensional (p.ej., cambiar el patrón del relleno)

unas propriedades avanzadas para un programa de pintar serían:

• se puede efectuar barridos a escala grande, es decir, se usa un pincel grueso
• se puede trabajar detalles a escala fina, es decir, se usa un pincel fino
• se puede realizar diferentes tipos de acciones:

  pintar encima:

  (``over'') se pinta el color del pincel según su transparencia encima de cada pixel, es decir, si el pincel no es transparente se cambia el pixel al color del pincel

  pintar debajo:

  (``under'') se pinta el color del pincel según la transparencia del fondo debajo de cada pixel, es decir, donde no hay transparencia no se cambia nada

  pintar dentro:

  (``in'') se aplica el color del pincel solamente en píxeles que ya fueron pintados

  borrar:

  (``erase'') se quita color de los píxeles según la transparencia del pincel

• el consumo de memoria debe depender meramente de la ``cantidad'' de detalles incorporados en la imagen (y no tanto de la resolución concreta)
• el tiempo de cálculo debe depender solamente de la escala en la cual se está trabajando
• el usuario debe tener la posibilidad de eligir cualquier escala para visualizar su trabajo

la idea principal consiste en usar la ondícula de Haar y la descomposición jerárquica (que resulta en una representación en forma de un árbol cuaternario o ``quadtree'')

se obtiene las siguientes ventajas:

• el número de coeficientes es igual al número de píxeles
• la ``navegación'' por el árbol permite una implementación sencilla de la composición de diferentes niveles
• la compresión implícita de la imagen (es decir, no guardar coeficientes igual a cero) reduce considerablemente el uso de memoria y permite trabajar directamente con la imagen comprimida sin previa expansión

las aplicaciones de tal sistema son más amplias

• sistema interactiva de manipular imágenes basadas en mapas de píxeles
• proyección de texturas a superficies dependiendo de la distancia del observador
• composición de imágenes dados en resoluciones diferentes

confinamos la discusión a imágenes cuadráticas con resoluciones de potencias de dos y no consideramos la extración eficiente de regiones

la estructura de datos del árbol cuaternario con los coeficientes de la descomposición se puede implementar como

class {
  rgba c;
  node root;
} quad_tree;

class {
  rgba      d[3];
  real      tau;
  quad_node child[4];

  rgba Decompose(int j, int x, int y);
  void Display(rgba c, int j) const;
  void DrawArea(rgba c) const;
  void Extrapolate(operation op, int x, int y);
  bool IsLeaf() const;
  int  Level() const;
} quad_node;

donde rgba es el tipo de datos de un pixel con sus cuatro canales rojo, verde, azul y alpha, y operacion es el tipo de datos para las operaciónes de pintar

la variable miembro tau será útil para la composición transparente que asumimos inicializada a 1

los coeficientes d[i] en cada nodo del árbol se obtienen calculando la descomposición jerárquica basado en la ondícula de Haar

cada nodo del árbol representa un área de la imagen, no hace falta guardar dicha área explícitamente porque sus coordenadas se puede derivar de la posición del nodo en el árbol

sin entrar en detalles asumimos que tengamos varios métodos

DrawArea(rgba c):

dibuja el área del nodo con el color pasado como parámetro

IsLeaf():

devuelve si el nodo es una hoja

Level():

devuelve el nivel del nodo en el árbol

el valor c de la raíz representa la media de todos los píxeles de la imagen

el árbol no está desarrollado al completo, nodos que contengan solamente coeficientes igual a cero están representados por punteros a nil

para editar una imagen hace falta tres operaciones básicas: visualizar, pintar, y actualizar (nota que no optimizamos para restringir las operaciones a la ventana/región donde de verdad hay que actuar)

visualizar:

si se quiere visualizar la imagen a nivel 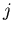$j$, es decir, en resolución 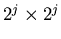$2^j\times 2^j$ se llama a la siguiente rutina recursiva:

void quad_node::Display(
  rgba c,
  int  j
) {
  rgba ci[4];
  ci[0]=c+d[0]+d[1]+d[2];
  ci[1]=c-d[0]+d[1]-d[2];
  ci[2]=c+d[0]-d[1]-d[2];
  ci[3]=c-d[0]-d[1]+d[2];
  for(int i(0); i<4; i++)
    if(IsLeaf() || Level()==j)
      child[i].DrawArea(ci[i]);
    else
      child[i].Display(ci[i],j+1);
}

es decir, se visualiza el área cuando se haya llegado o bien a una hoja del árbol o bien al nivel deseado, el color que se usa para visualizar se calcula acumulando los detalles de cada nodo

nota que se hace como mucho una operación por pixel

pintar:

las operaciónes se realiza de la siguiente manera

• para las acciones del usuario se usa un plano independiente a la imagen que tiene la resolución que vea el usuario, este plano se puede ver como un búfer encima de la imagen visualizada
• mientras el usuario no cambia el tipo de operación ni la resolución o la posición de la visualización se actua sobre dicho búfer sin cambiar la la imagen debajo
• una vez que hay un dicho cambio se actualiza la imagen debajo (es decir, se propaga el contenido del búfer a la estructura del árbol cuaternario) y se vacía el búfer

(falta descripción)

actualizar:

(falta descripción)

rgba quad_node::Decompose(
  int j,
  int x,
  int y
) {
  if(Level()==j) return R.C(x,y);
  rgba ci[4];
  for(int i(0); i<4; i++)
    ci[i]=child[i].Decompose(j,x,y);

  d[0]=(ci[0]-ci[1]+ci[2]-ci[3])/4;
  d[1]=(ci[0]+ci[1]-ci[2]-ci[3])/4;
  d[2]=(ci[0]-ci[1]-ci[2]+ci[3])/4;
  return (ci[0]+ci[1]+ci[2]+ci[3])/4;
}

(falta descripción)

void quad_node::Extrapolate(
  operation op,
  int       x,
  int       y
) {
  for(int i(0); i<3; i++)
    switch(op) {
      case over: 
        d[i]*=1.0-F(x,y).c.alpha;
        break;
      case under:
        d[i]-=d[i].alpha*F(x,y).c;
        break;
      case in:   
        d[i] =d[i]*(1.0-F(x,y).c.alpha)+d[i].alpha*F(x,y).c;
        break;
      case erase:
        d[i]*=1.0-F.delta(x,y);
        break;
    }
  if(!IsLeaf())
    for(int i(0); i<4; i++)
      child[i].Extrapolate(op,x,y);
}

(falta descripción)