Umbralisación simples

el método más simple para obtener una cuantificación y codificación de los coeficientes (que resultan en una compresión con pérdidas) es la siguiente:

• se elimina todos aquellos coeficientes que no superan algún umbral predeterminado
• se cuantifica los coeficientes restantes con un cuantificador escalar estándar
• se codifica la secuencia de valores resultantes (con muchos ceros) con un codificador sin redundancia como descritos arriba

si queremos controlar un poco el error que se comete en vez de asumir un umbral $\tau$ predetermindado podemos actuar como sigue:

primero asumimos que la transformada calculada es una aproximación suficientemente bien a la imagen original, es decir

$$\begin{eqnarray*} \Vert\sum_kc_k\psi_k-I\Vert&\approx&0 \end{eqnarray*}$$

(para simplificar la notación, enumeramos todas las funciones bases ortonormales participando en la transformación con un índice $k$ y las llamamos $\psi$)

ya sabemos que los coeficientes pequeños son los posibles candidatos para ser eliminados, por eso ordenamos los $m$ coeficientes de la transformada de una imagen con $m$ píxels en orden descendente, es decir, obtenemos

$$c_{\pi(0)}>c_{\pi(1)}>c_{\pi(2)}>\dots>c_{\pi(m-1)}$$

indicando $\pi$ la permutación de índices

si eliminamos a partir de algún índice $\hat m$ los coeficientes cometemos el error

$$\begin{eqnarray*} \Vert\sum_{k=0}^{m-1}c_{\pi(k)}\psi_{\pi(k)}-\sum_{k=\hat 0}^... ...\pi(l)}\Vert^2\rangle \\ &=& \sum_{k=\hat m}^{m-1}c_{\pi(k)}^2 \end{eqnarray*}$$

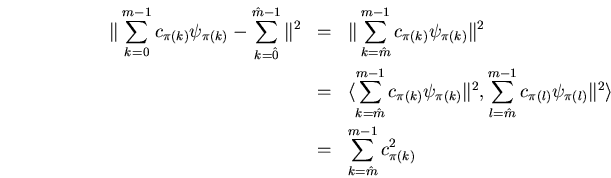
entonces eliminamos los coeficientes pequeños empezando desde el índice $\pi(m-1)$ hacia $\pi(0)$ mientras que la suma sea menor que algún $\epsilon^2$ relacionado con la máxima relación entre señal y error (pSNR) que queremos permitir

porque la ordenación requiere para imágenes grandes mucho tiempo y espacio (necesitamos guardar la permutación) es más aprobriado realizar una búsqueda binaria para encontrar el umbral idóneo:

• buscamos el coeficiente más grande y el coeficiente más pequeño
• efectuamos una búsqueda binaria sobre este intervalo donde el criterio de decisión está basado en el error cometido descartar todos los coeficientes menor que el centro del intervalo