Idea

• representar funciones (secuencias) de forma jerárquica
• usar coeficientes que proporcionan ``alguna'' información para ambas cosas: lugar y frecuencia

un método: ondículas

representación de una función a escala grande con coeficientes adicionales para describir los detalles, y eso de forma jerárquica

existe una estrecha relación entre las áreas

• transformada de ondículas
• teoría de filtros de señales
• análisis multiresolución
• algoritmos de pirámides
• codificación con sub-bandas

transformaciones

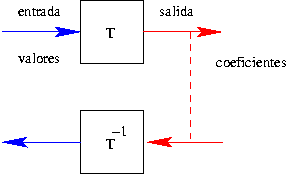
reversible

propriedades de la transformada con ondículas

• tiempo de cálculo lineal en número de datos (casos discretos y prácticos)
• muchos coeficientes tienden (en casos prácticos) a valores muy pequeños o cero
• se adaptan bien a discontinuidades y dominios limitados

análisis multiresolución (multi-resolution analysis)

representación de una función con un conjunto de funciones bases (llamados ondículas) que son versiones escaladas y trasladadas de la misma función (ondícula madre, mother wavelet)

en el caso continuo la transformada de ondículas es invariante a translados de la función bajo estudio, eso no es el caso con secuencias sobre un dominio limitado