la transformada de ![]() trabaja con secuencias de números reales
y está relacionado con la transformación de Laplace que trabaja
con señales continuas, más concreto:
trabaja con secuencias de números reales
y está relacionado con la transformación de Laplace que trabaja
con señales continuas, más concreto:
sea
![]() una secuencia de números reales, es decir,
una secuencia de números reales, es decir,
![]() , se asigna a la secuencia la serie
, se asigna a la secuencia la serie

con ![]() que en caso de su convergencia se define como la transformada de
que en caso de su convergencia se define como la transformada de ![]() de la secuencia
de la secuencia
por ejemplo,

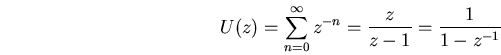
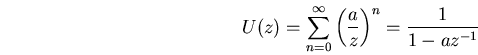
si la secuencia
![]() es finita, es decir,
es finita, es decir,
![]() ,
tenemos series geométricas finitas, para los ejemplos:
,
tenemos series geométricas finitas, para los ejemplos:
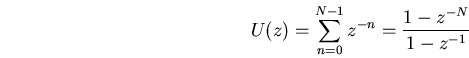
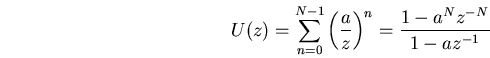
formalmente se puede ampliar las definiciones para tratar también
secuencias
![]() que nos llevarían a series de Laurent
(que son polinomios que permiten exponentes positivos y negativos),
este asunto es importante si tratamos la convolución de secuencias.
que nos llevarían a series de Laurent
(que son polinomios que permiten exponentes positivos y negativos),
este asunto es importante si tratamos la convolución de secuencias.
anotamos algunas propriedades de la transformada de ![]() que son
importantes en nuestro contexto:
que son
importantes en nuestro contexto:
escribimos la nueva secuencia como
![]() :
:
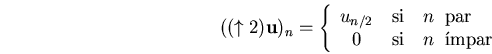
para la transformado de ![]() de la secuencia
de la secuencia ![]() obtenemos
obtenemos
que se ve usando las definiciones
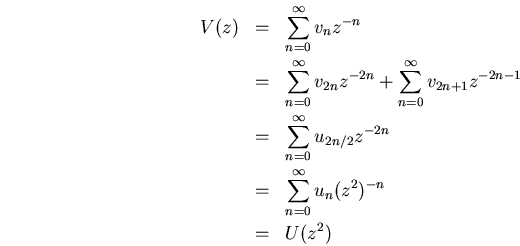
escribimos la nueva secuencia como
![]() :
:
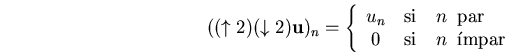
para la transformado de ![]() de la secuencia
de la secuencia ![]() obtenemos
obtenemos
que se ve usando las definiciones
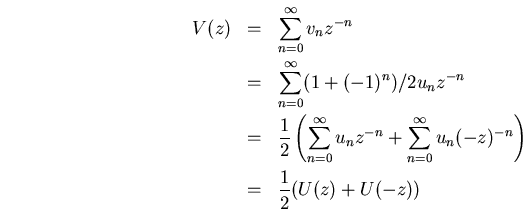

dadas dos secuencias ![]() y
y ![]() con sus transformadas de
con sus transformadas de ![]()
![]() y
y ![]() , obtenemos para la convolución
, obtenemos para la convolución
es decir, la convolución de las dos secuencias resulta en una
multiplicación de sus transformadas de ![]()
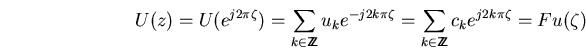
es decir, justamente la transformado de Fourier
con los coeficientes de Fourier ![]()