- Unión:
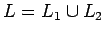 es libre de contexto, porque podemos construir
a partir de las gramáticas
es libre de contexto, porque podemos construir
a partir de las gramáticas
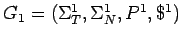 y
y
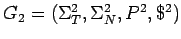 con
con 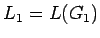 y
y 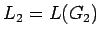 la gramática
la gramática
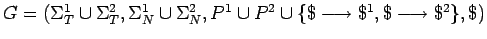 que es una gramática libre de contexto y obviamente genera todas
las palabras tanto en
que es una gramática libre de contexto y obviamente genera todas
las palabras tanto en 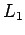 como en
como en 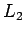 .
.
Eso no es el caso si nos limitamos a los lenguajes libres de contexto
deterministas.
- Concatención:
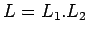 es libre de contexto, porque podemos construir
a partir de las gramáticas
es libre de contexto, porque podemos construir
a partir de las gramáticas
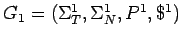 y
y
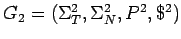 con
con 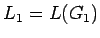 y
y 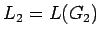 la gramática
la gramática
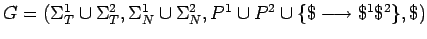 que es una gramática libre de contexto y obviamente genera todas
las palabras en
que es una gramática libre de contexto y obviamente genera todas
las palabras en  .
.
Eso no es el caso si nos limitamos a los lenguajes libres de contexto
deterministas.
- Clausura:
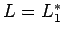 es libre de contexto, porque podemos construir
una gramática libre de contexto a partir de la gramática para
es libre de contexto, porque podemos construir
una gramática libre de contexto a partir de la gramática para 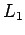 ,
simplemente añadimos las producciones
,
simplemente añadimos las producciones
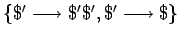 siendo
siendo 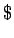 el nuevo símbolo inicial.
el nuevo símbolo inicial.
- Intersección:
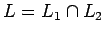 no es libre de contexto (en general), como demuestra el
ejemplo:
no es libre de contexto (en general), como demuestra el
ejemplo:
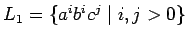 y
y
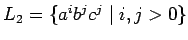 nos lleva a
nos lleva a
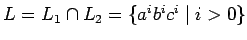 que no es libre de contexto
como ya vimos.
que no es libre de contexto
como ya vimos.
Si confinamos 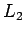 a lenguajes regulares, entonces la intersección
produce lenguajes libres de contexto. El argumento es igual de
constructivo como en el caso de dos lenguajes regulares.
a lenguajes regulares, entonces la intersección
produce lenguajes libres de contexto. El argumento es igual de
constructivo como en el caso de dos lenguajes regulares.
- Complemento:
-
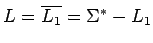 no es libre de contexto (en general),
porque si asumimos que lo fuera y sabiendo que la unión lo es
podríamos derivar
no es libre de contexto (en general),
porque si asumimos que lo fuera y sabiendo que la unión lo es
podríamos derivar
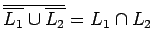 como
libre de contexto, pero ya sabemos que la intersección no genera
siempre tal lenguajes.
como
libre de contexto, pero ya sabemos que la intersección no genera
siempre tal lenguajes.
Para los lenguajes libres de contexto determinista, el complemento
genera un lenguaje libre de contexto determinista, porque es fácil
invertir un autómata determinista.
- Diferencia:
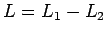 no es libre de contexto (en general), porque
no es libre de contexto (en general), porque
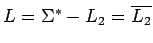 no es libre de contexto.
no es libre de contexto.
![]() y
y ![]() dos lenguajes libres de contexto.
dos lenguajes libres de contexto.
![]() a lenguajes regulares, entonces la intersección
produce lenguajes libres de contexto. El argumento es igual de
constructivo como en el caso de dos lenguajes regulares.
a lenguajes regulares, entonces la intersección
produce lenguajes libres de contexto. El argumento es igual de
constructivo como en el caso de dos lenguajes regulares.
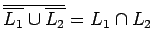 como
libre de contexto, pero ya sabemos que la intersección no genera
siempre tal lenguajes.
como
libre de contexto, pero ya sabemos que la intersección no genera
siempre tal lenguajes.