



Siguiente: Algoritmos de decisión de
Subir: Propiedades, algoritmos de decisión,
Anterior: Propiedades, algoritmos de decisión,
Índice General
Sean 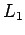 y
y 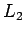 dos lenguajes regulares.
dos lenguajes regulares.
- Unión:
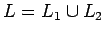 es regular, porque podemos construir
una expresión regular para
es regular, porque podemos construir
una expresión regular para  , teniendo las expresiones regulares
para
, teniendo las expresiones regulares
para 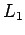 y
y 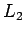 , más preciso: con
, más preciso: con 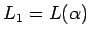 y
y 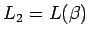 tenemos
tenemos
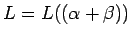
- Concatención:
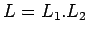 es regular, porque podemos construir
una expresión regular para
es regular, porque podemos construir
una expresión regular para  , teniendo las expresiones regulares
para
, teniendo las expresiones regulares
para 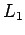 y
y 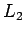 , más preciso: con
, más preciso: con 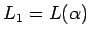 y
y 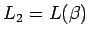 tenemos
tenemos
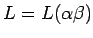
- Clausura:
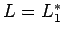 es regular, porque podemos construir
una expresión regular para
es regular, porque podemos construir
una expresión regular para  , teniendo la expresión regular
para
, teniendo la expresión regular
para 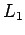 , más preciso: con
, más preciso: con 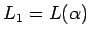 tenemos
tenemos
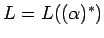
- Complemento:
-
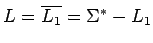 es regular, porque podemos construir,
dado un AFD completo
es regular, porque podemos construir,
dado un AFD completo 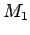 que acepta
que acepta 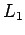 , un AFD
, un AFD  que acepta
que acepta
 simplemente `invertiendo' sus estados finales, es decir,
los estados no finales de
simplemente `invertiendo' sus estados finales, es decir,
los estados no finales de 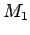 serán los estados finales de
serán los estados finales de  y los finales se convierten en los no finales, entonces,
si
y los finales se convierten en los no finales, entonces,
si
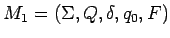 construimos
construimos
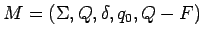 .
.
- Intersección:
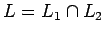 es regular, porque con las reglas de DeMorgan
obtenemos
es regular, porque con las reglas de DeMorgan
obtenemos
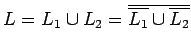 .
Complemento y unión producen lenguajes regulares, como visto antes.
Dicha construcción es bastante laborosa, abajo vemos una construcción
directa y simple.
.
Complemento y unión producen lenguajes regulares, como visto antes.
Dicha construcción es bastante laborosa, abajo vemos una construcción
directa y simple.
- Diferencia:
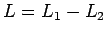 es regular, porque se puede expresar la diferencia como
es regular, porque se puede expresar la diferencia como
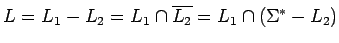 y las
operaciones usadas mantienen la regularidad.
y las
operaciones usadas mantienen la regularidad.
En vez de usar la lógica booleana, es decir, aplicando las
reglas de DeMorgan, se puede construir directamente un autómata
que acepta el lenguaje 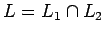 .
.
La idea principal es, simular en paralelo en un solo autómata (digamos
autómata de producto) las transiciones de los
dos autómatas (por ejemplo finitos deterministas y completas)
para 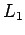 y
y 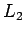 .
.
Entonces sean
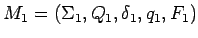 y
y
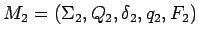 los dos AFDs completos que
aceptan
los dos AFDs completos que
aceptan 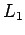 y
y 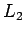 , es decir,
, es decir, 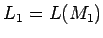 y
y 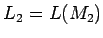 .
.
Construimos el AFD completo  que acepta
que acepta
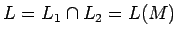 como
como
donde
Ejemplo:

Obviamente la construcción funciona igual con autómatas finitos
no-deterministas (AFND).
- Homomorfismo:
- a lo mejor lo incluyo.




Siguiente: Algoritmos de decisión de
Subir: Propiedades, algoritmos de decisión,
Anterior: Propiedades, algoritmos de decisión,
Índice General
© 2006, Dr. Arno Formella, Universidad de Vigo, Departamento de Informática
![]() y
y ![]() dos lenguajes regulares.
dos lenguajes regulares.
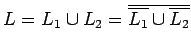 .
Complemento y unión producen lenguajes regulares, como visto antes.
Dicha construcción es bastante laborosa, abajo vemos una construcción
directa y simple.
.
Complemento y unión producen lenguajes regulares, como visto antes.
Dicha construcción es bastante laborosa, abajo vemos una construcción
directa y simple.
![]() .
.
![]() y
y ![]() .
.
![]() y
y
![]() los dos AFDs completos que
aceptan
los dos AFDs completos que
aceptan ![]() y
y ![]() , es decir,
, es decir, ![]() y
y ![]() .
.
![]() que acepta
que acepta
![]() como
como
![]()