



Siguiente: Propiedades, algoritmos de decisión,
Subir: Lenguajes regulares
Anterior: Equivalencia entre gramáticas lineales
Índice General
Siendo 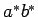 una expresión regular, podemos construir un autómata
finito que acepta el lenguaje así definido, también podemos construir
para cualquier
una expresión regular, podemos construir un autómata
finito que acepta el lenguaje así definido, también podemos construir
para cualquier 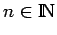 fijo un autómata finito adecuado
(
fijo un autómata finito adecuado
(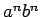 sería una expresión regular extendida que define el
lenguaje correspondiente que contiene una sola palabra).
sería una expresión regular extendida que define el
lenguaje correspondiente que contiene una sola palabra).
Pero no podemos construir un autómata finito que acepte el
lenguaje:
donde el parámetro 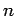 no es fijo, sino se quiere que haya tantas
no es fijo, sino se quiere que haya tantas
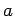 's como
's como 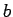 's.
's.
¿Por qué no podemos construir tal autómata?
Observamos el comportamiento del siguiente autómata:
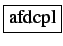
Lema (de bombeo para lenguajes regulares):
Sea  un lenguaje regular (infinito).
Entonces existe un
un lenguaje regular (infinito).
Entonces existe un 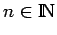 de tal manera que cada palabra
de tal manera que cada palabra
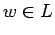 con
con 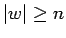 se puede dividir en tres partes,
se puede dividir en tres partes, 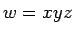 cumpliéndose las tres propiedades:
cumpliéndose las tres propiedades:
-
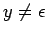
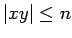
- para todos los
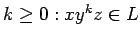
Comprobación (ideas principales):
- Sea
 un lenguaje regular (infinito).
un lenguaje regular (infinito).
- Entonces existe un autómata finito determinista
 que acepta
que acepta  .
.
- Sea
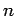 el número de estados de
el número de estados de  (
(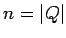 ).
).
- Sea
 una palabra con
una palabra con 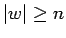 (tal palabra existe porque
(tal palabra existe porque  es infinito).
es infinito).
- Entonces se visita un estado de
 por lo menos dos veces.
por lo menos dos veces.
- Escogemos el estado que se visita la primera vez dos veces,
le llamamos
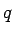 .
.
- La parte de
 que se lee hasta llegar la primera vez a
que se lee hasta llegar la primera vez a 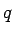 llamamos
llamamos
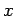 (puede ser que
(puede ser que 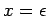 ).
).
- La parte de
 que se lee hasta llegar la segunda vez a
que se lee hasta llegar la segunda vez a 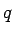 llamamos
llamamos
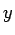 (
(
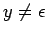 porque un bucle en un AFD tiene aristas con símbolos).
porque un bucle en un AFD tiene aristas con símbolos).
- La longitud
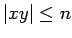 porque hemos recorrido un camino dondo solo
un estado aparece dos veces.
porque hemos recorrido un camino dondo solo
un estado aparece dos veces.
- La parte que sobra para terminar aceptando
 llamamos
llamamos 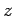 .
.
- Entonces dividimos
 en tres partes, es decir,
en tres partes, es decir, 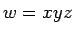 .
.
 acepta tanto
acepta tanto 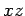 , como
, como 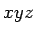 , como cualquier
, como cualquier 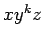 para
todos los
para
todos los 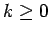 porque podemos recorrer el bucle de
porque podemos recorrer el bucle de 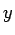 tantas veces
como queremos (esto se debe comprobar formalmente con inducción).
tantas veces
como queremos (esto se debe comprobar formalmente con inducción).
Entonces, comprobamos de nuevo que 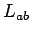 no es regular, ahora
usando el lema de bombeo:
no es regular, ahora
usando el lema de bombeo:
- Asumimos que
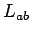 sea regular.
sea regular.
- El lema de bombeo nos garantiza la existencia de un
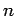 tal que
se cumplen las propiedades para palabras
tal que
se cumplen las propiedades para palabras  con
con 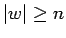 .
.
- (Pensamos...): Elegimos
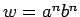 . Obviamente
. Obviamente 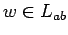 y
y
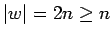 .
.
- El lema de bombeo nos garantiza la existencia de una partición
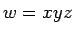 con
con
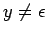 ,
, 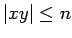 ,
y
,
y
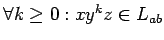 .
(No conocemos la partición en concreto, pero sus propiedades.)
.
(No conocemos la partición en concreto, pero sus propiedades.)
- Porque
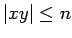 el prefijo
el prefijo 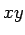 no contiene ninguna
no contiene ninguna 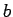 .
.
- Porque
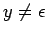 la subpalabra
la subpalabra 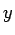 contiene por lo menos una
contiene por lo menos una 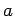 .
.
- Todos las
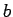 s están en
s están en 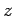 .
.
- Tanto
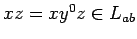 como
como
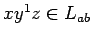 pero
pero 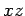 contiene
por lo menos una
contiene
por lo menos una 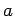 menos que
menos que 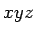 (hemos quitado
(hemos quitado 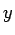 ).
).
- Eso es una contradicción porque
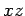 no debe estar dentro
no debe estar dentro 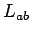 .
.
- Entonces
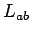 no puede ser regular.
no puede ser regular.
Receta para el uso del lema de bombeo:
- Dado un lenguaje
 .
.
- Queremos comprobar que
 no es regular.
no es regular.
- Comprobación con contradicción.
- Asumimos que
 sea regular.
sea regular.
- El lema de bombeo garantiza la existencia de un
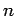 (pero no lo conocemos).
(pero no lo conocemos).
- Buscamos
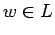 (con un poco de sabiduría) que depende de
(con un poco de sabiduría) que depende de 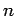 , tal
que
, tal
que 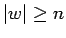
- El lema de bombeo garantiza la existencia de la partición de
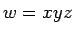 cumpliendo las 3 propiedades.
cumpliendo las 3 propiedades.
- Comprobamos (con un poco de sabiduría) que, independiente
de la partición de
 en concreto (en los límites de las primeras
dos propiedades), se produce una contradicción con la tercera
propiedad.
en concreto (en los límites de las primeras
dos propiedades), se produce una contradicción con la tercera
propiedad.
Podemos describir dicha `receta' también como un juego para dos
personas:
- Juego para un lenguaje
 .
.
- Jugador 1 selecciona
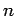 .
.
- Jugador 2 selecciona
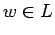 con
con 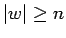 .
.
- Jugador 1 selecciona partición
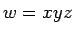 con
con
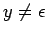 y
y 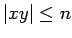 .
.
- Jugador 2 selecciona
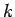 .
.
- si
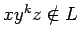 gana jugador 2, sino gana jugador 1.
gana jugador 2, sino gana jugador 1.
- si jugador 2 puede ganar siempre, entonces
 no es regular.
no es regular.
El lema de bombeo es el jugador 1, ¿quién es el jugador 2?
Otro Ejemplo:
es decir, todas las cadenas de ceros que tienen un número cuadrado
de símbolos.
Dos comentarios más:
- Este lema de bombeo solo garantiza una propiedad para lenguajes
regulares, es decir, todos los lenguajes regulares (infinitos) la tienen,
pero pueden existir más lenguajes que la tengan, o en otras palabras,
pueden existir lenguajes
 donde encontramos tal
donde encontramos tal 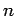 y la división de
y la división de
 en
en 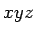 con todas las propiedades, pero
con todas las propiedades, pero  no es regular.
no es regular.
- Con el lema de bombeo también se puede derivar: si tal
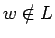 entonces
entonces 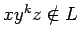 (el argumento es fácil: no hace falta que
lleguemos a una estado final en la comprobación, lo importante eran
los caminos recorridos).
(el argumento es fácil: no hace falta que
lleguemos a una estado final en la comprobación, lo importante eran
los caminos recorridos).
Reglas de mano:
- Un lenguaje es regular si independientemente de la longitud de
la palabra de entrada, hay que memorizar solamente una cantidad constante
de información (en el caso de
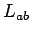 deberíamos memorizar el número
de
deberíamos memorizar el número
de 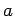 's que no es constante).
's que no es constante).
- La comprobación formal se realiza con el lema de bombeo.
- El lema de bombeo se usa para comprobar que un lenguaje no
es regular, para comprobar que es regular, por ejemplo,
se construye un autómata finito,
una expresión regular, o una grámatica de tipo 3.
Pero ojo, existen lenguajes regulares que tienen que ver con números:
Ejercicio: contruye un autómata finito que acepte 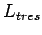 .
.




Siguiente: Propiedades, algoritmos de decisión,
Subir: Lenguajes regulares
Anterior: Equivalencia entre gramáticas lineales
Índice General
© 2006, Dr. Arno Formella, Universidad de Vigo, Departamento de Informática
![]() una expresión regular, podemos construir un autómata
finito que acepta el lenguaje así definido, también podemos construir
para cualquier
una expresión regular, podemos construir un autómata
finito que acepta el lenguaje así definido, también podemos construir
para cualquier ![]() fijo un autómata finito adecuado
(
fijo un autómata finito adecuado
(![]() sería una expresión regular extendida que define el
lenguaje correspondiente que contiene una sola palabra).
sería una expresión regular extendida que define el
lenguaje correspondiente que contiene una sola palabra).
![]() no es fijo, sino se quiere que haya tantas
no es fijo, sino se quiere que haya tantas
![]() 's como
's como ![]() 's.
's.
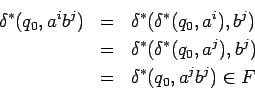
![]()
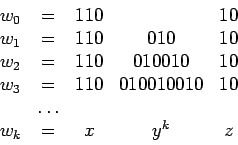
![]() un lenguaje regular (infinito).
Entonces existe un
un lenguaje regular (infinito).
Entonces existe un ![]() de tal manera que cada palabra
de tal manera que cada palabra
![]() con
con ![]() se puede dividir en tres partes,
se puede dividir en tres partes, ![]() cumpliéndose las tres propiedades:
cumpliéndose las tres propiedades:
![]() no es regular, ahora
usando el lema de bombeo:
no es regular, ahora
usando el lema de bombeo:

![]() .
.