



Siguiente: Equivalencia entre gramáticas lineales
Subir: Lenguajes regulares
Anterior: Lenguajes regulares
Índice General
Sea
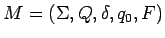 un AFD.
un AFD.
Construimos una gramática lineal por la derecha 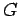 con
con 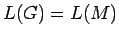 ,
es decir, genera el mismo lenguaje que el AFD acepta.
,
es decir, genera el mismo lenguaje que el AFD acepta.
es decir
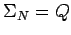 , los estados del autómata determinan los símbolos
no-terminales de la gramática
, los estados del autómata determinan los símbolos
no-terminales de la gramática
-
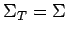 , los símbolos del autómata determinan los
símbolos terminales de la gramática
, los símbolos del autómata determinan los
símbolos terminales de la gramática
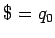 , el estado inicial del autómata determina el
símbolo inicial de la gramática
, el estado inicial del autómata determina el
símbolo inicial de la gramática
El sistema de producciones 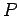 está dado por:
está dado por:
- Si
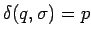 es una transición del AFD, con
es una transición del AFD, con 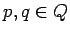 y
y
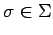 , entonces añadimos a
, entonces añadimos a 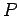 la producción
la producción
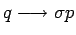 .
.
- Si
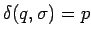 es una transición del AFD, con
es una transición del AFD, con 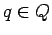 ,
,
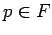 y
y
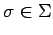 , entonces añadimos a
, entonces añadimos a 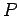 la producción
la producción
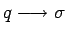 .
.
- Si
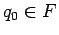 , entonces añadimos a
, entonces añadimos a 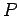 la producción
la producción
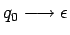 .
.
Ejemplo:

Entonces el sistema de producciones 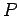 de la gramática será:
de la gramática será:
Sea
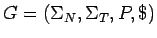 una gramática lineal por la derecha,
es decir,
una gramática lineal por la derecha,
es decir,
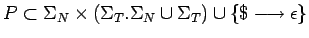 .
.
Construimos una autómata finito  con
con 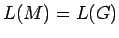 , es decir, el autómata acepta
el mismo lenguaje que la gramática genera.
, es decir, el autómata acepta
el mismo lenguaje que la gramática genera.
es decir,
-
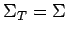 , los símbolos terminales de la gramática
determinan los símbolos del autómata
, los símbolos terminales de la gramática
determinan los símbolos del autómata
-
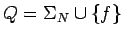 , los símbolos no-terminales de la gramática
determinan los estados del autómata,
y añadimos un nuevo estado
, los símbolos no-terminales de la gramática
determinan los estados del autómata,
y añadimos un nuevo estado  , es decir,
, es decir,
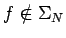
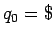 , el símbolo inicial de la gramática determina el
estado inicial del autómata
, el símbolo inicial de la gramática determina el
estado inicial del autómata
Las transiciones 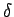 están dadas por:
están dadas por:
- Si
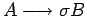 es una producción de
es una producción de 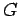 , con
, con
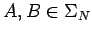 y
y
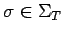 , entonces añadimos la transición
, entonces añadimos la transición
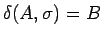 .
.
- Si
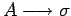 es una producción de
es una producción de 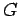 , con
, con 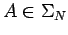 y
y
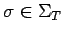 , entonces añadimos la transición
, entonces añadimos la transición
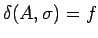 .
.
- Si
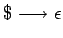 es una producción de
es una producción de 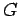 ,
entonces añadimos la transición
,
entonces añadimos la transición
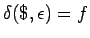 .
.
Observamos que el autómata construido es un autómata finito
no-determinista (AFND) que podemos convertir en un AFD si hace falta.
Ejemplo:
Para la gramática de arriba--renombrando los símbolos--convertimos
a la tabla de transiciones





Siguiente: Equivalencia entre gramáticas lineales
Subir: Lenguajes regulares
Anterior: Lenguajes regulares
Índice General
© 2006, Dr. Arno Formella, Universidad de Vigo, Departamento de Informática
![]() un AFD.
un AFD.
![]() con
con ![]() ,
es decir, genera el mismo lenguaje que el AFD acepta.
,
es decir, genera el mismo lenguaje que el AFD acepta.
![]() está dado por:
está dado por:
![]()
![]() de la gramática será:
de la gramática será:
![]() una gramática lineal por la derecha,
es decir,
una gramática lineal por la derecha,
es decir,
![]() .
.
![]() con
con ![]() , es decir, el autómata acepta
el mismo lenguaje que la gramática genera.
, es decir, el autómata acepta
el mismo lenguaje que la gramática genera.
![]() están dadas por:
están dadas por:
![]()