



Siguiente: Equivalencia entre autómatas finitos
Subir: Expresiones regulares
Anterior: Expresiones regulares
Índice General
Sea 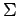 un alfabeto.
Una expresión regular
un alfabeto.
Una expresión regular 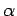 sobre
sobre 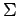 se
define con las siguientes reglas (inductivas):
se
define con las siguientes reglas (inductivas):
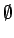 es una expresión regular
es una expresión regular
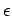 es una expresión regular
es una expresión regular
- si
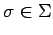 , entonces
, entonces 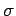 es una expresión regular
es una expresión regular
- si
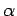 y
y 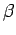 son expresiones regulares, entonces
también
son expresiones regulares, entonces
también
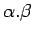 es una expresión regular (obviamos
del punto muchas veces)
es una expresión regular (obviamos
del punto muchas veces)
-
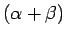 es una expresión regular
es una expresión regular
- si
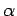 es una expresión regular, entonces
también
es una expresión regular, entonces
también
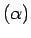 es una expresión regular
es una expresión regular
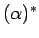 es una expresión regular
es una expresión regular
Como observamos: hemos introducido meta-símbolos
(`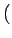 ',`
',`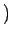 ',`
',`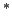 ',`
',`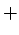 ',`
',` ',`
',`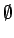 ').
Si alguno de ellos aparece en
').
Si alguno de ellos aparece en 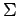 tenemos un problema (Houston)
que resolveremos al final de esta sección.
tenemos un problema (Houston)
que resolveremos al final de esta sección.
Ejemplos:
Sea
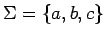 . Posibles expresiones regulares son:
. Posibles expresiones regulares son:
Con eso hemos definido una síntaxis de expresiones regulares,
pero ¿cuál será su semántica?
Para cada expresión regular definimos un lenguaje correspondiente
(basado en las reglas).
El lenguaje 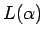 definido por una expresión regular
definido por una expresión regular
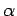 se define:
se define:
-
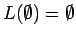
-
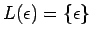
- si
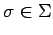 , entonces
, entonces
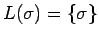
- si
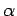 y
y 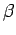 son expresiones regulares, entonces
son expresiones regulares, entonces
-
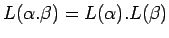
-
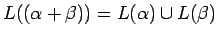
- si
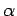 es una expresión regular
es una expresión regular
-
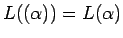
-

Ejemplos: sobre
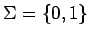 :
:




Siguiente: Equivalencia entre autómatas finitos
Subir: Expresiones regulares
Anterior: Expresiones regulares
Índice General
© 2006, Dr. Arno Formella, Universidad de Vigo, Departamento de Informática
![]() un alfabeto.
Una expresión regular
un alfabeto.
Una expresión regular ![]() sobre
sobre ![]() se
define con las siguientes reglas (inductivas):
se
define con las siguientes reglas (inductivas):
![]() ',`
',`![]() ',`
',`![]() ',`
',`![]() ',`
',`![]() ',`
',`![]() ').
Si alguno de ellos aparece en
').
Si alguno de ellos aparece en ![]() tenemos un problema (Houston)
que resolveremos al final de esta sección.
tenemos un problema (Houston)
que resolveremos al final de esta sección.
![]() . Posibles expresiones regulares son:
. Posibles expresiones regulares son:
![]() definido por una expresión regular
definido por una expresión regular
![]() se define:
se define:
![]() :
: