Mittelpunkt-Entscheidungsalgorithmus

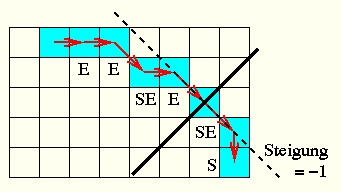
Ähnlich wie beim Zeichnen eines Kreises, allerdings zeichnen wir direkt einen Quadranten!

treffen erst sukkzessive Entscheidungen bis die Steigung -1 erreicht ist, ob nächstes Pixel im Osten (E) oder im Südosten (SE) ?

treffen dann sukkzessive Entscheidungen, ob nächstes Pixel im Südosten (SE) oder im Süden (S) ?

untersuchen hierzu Mittelpunkt zwischen den entsprechenden Pixeln durch Einsetzen in die implizite Form

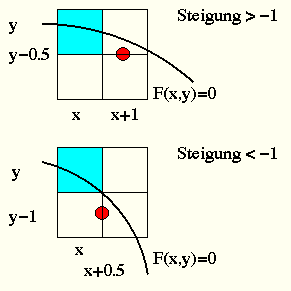
Wann beträgt die Steigung -1?

Bemühen wir die Tangentengleichung:

$$\begin{eqnarray*} (x-x_0)\cdot\underbrace{\frac{\partial F(x_0,y_0)}{\partial x}... ...frac{\partial F(x_0,y_0)}{\partial y}}_{\displaystyle =dy} &=& 0 \end{eqnarray*}$$

Transformation dieser impliziten Geradengleichung in die explizite Form:

$$\begin{eqnarray*} 0 &=& (x-x_0)\cdot dx+ (y-y_0)\cdot dy \\ 0 &=& xdx-x_0dx+ydy... ...dx}{dy} - x\cdot \frac{dx}{dy}\\ y &=& y_0-(x-x_0)\frac{dx}{dy} \end{eqnarray*}$$

Die Steigung ist also

$$\begin{eqnarray*} \mbox{}-\frac{dx}{dy} &=&\mbox{}-\frac{\displaystyle\frac{\pa... ...rtial x}} {\displaystyle\frac{\partial F(x_0,y_0)}{\partial y}} \end{eqnarray*}$$

d.h. die Steigung ist gleich -1, wenn für die partiellen Ableitungen gilt:

$$\begin{eqnarray*} \partial F/\partial x&=&\partial F/\partial y \end{eqnarray*}$$

Berechnen wir dies:

$$\begin{eqnarray*} F(x,y) &=& r_y^2x^2+r_x^2y^2-r_x^2r_y^2 \\ & &\\ \partial ... ... 2r_y^2x \\ & &\\ \partial F(x,y)/\partial y &=& 2r_x^2y \\ \end{eqnarray*}$$

Überraschung: wenn wir $r_x=r_y=r$ wählen, entspricht dies genau der Bedingung beim Kreiszeichnen: $x=y$

 
void DrawEllipseQuadrant(
  int x0, int y0,
  int rx, int ry,
  int color
) {
  int x(0);
  int y(ry);

  SetPixel(x+x0, y+y0, color);
  while( 2*ry*ry*x < 2*rx*rx*y ) {
    if( F(x+1, y-0.5) >= 0) y--;
    x++;
    SetPixel(x+x0, y+y0, color);
  }
  while( y >= 0 ) {
    if( F(x+0.5, y-1) <= 0) x++;
    y--;
    SetPixel(x+x0, y+y0, color);
  }
}

Statt $F(x,y)$ immer wieder komplett zu berechen, nutze bereits berechnete Werte aus vorhergehender Iteration!

erster Oktant:

 

• Fall E:
  $$\begin{eqnarray*} \lefteqn{F(x+2,y-0.5)-F(x+1,y-0.5)} \\ &=& r_y^2(x+2)^2+r_x... ...r_x^2r_y^2 \\ &=& 2r_y^2x+3r_y^2 \\ &=& 2r_y^2(x+1)+r_y^2 \end{eqnarray*}$$
  
  
  
  
  

• Fall SE:
  $$\begin{eqnarray*} \lefteqn{F(x+2,y-1.5)-F(x+1,y-0.5)} \\ &=& r_y^2(x+2)^2+r_x... ...2x+3r_y^2-2r_x^2y+2r_x^2 \\ &=& 2r_y^2(x+1)+r_y^2-2r_x^2(y-1) \end{eqnarray*}$$
  
  
  
  
  

zweiter Oktant:

 

• Fall SE:
  $$\begin{eqnarray*} \lefteqn{F(x+1.5,y-2)-F(x+0.5,y-1)} \\ &=& r_y^2(x+1.5)^2+r... ...2x+2r_y^2-2r_x^2y+3r_x^2 \\ &=& 2r_y^2(x+1)-2r_x^2(y-1)+r_x^2 \end{eqnarray*}$$
  
  
  
  
  

• Fall S:
  $$\begin{eqnarray*} \lefteqn{F(x+0.5,y-2)-F(x+0.5,y-1)} \\ &=& r_y^2(x+0.5)^2+r... ... &=& \mbox{}-2r_x^2y+3r_x^2 \\ &=& \mbox{}-2r_x^2(y-1)+r_x^2 \end{eqnarray*}$$
  
  
  
  
  

Zu Beginn:

 

$$\begin{eqnarray*} \lefteqn{F(1,r_y-0.5)} \\ &=& r_y^2+r_x^2(r_y-0.5)^2-r_x^2r_y^2 \\ &=& r_y^2-r_x^2r_y+1/4\cdot r_x^2 \end{eqnarray*}$$

Auch hier runden wir, statt mit 4 zu multiplizieren.

Macht man dabei einen groben Fehler?: Übung.

Übergang vom ersten zum zweiten Quadranten:
Werten $F(x+0.5,y-1)$ bezüglich der zuletzt gesetzten Position aus.

$$\begin{eqnarray*} \lefteqn{F(x+0.5,y-1)} \\ &=& r_y^2(x+0.5)^2+r_x^2(y-1)^2-r_x^2r_y^2 \end{eqnarray*}$$

Bemerkung: hier könnten wir die Zeichenrichtung umdrehen und an der $x$-Achse zu zeichnen beginnen. Dies würde die Berechnungen zwischen den Quadranten etwas vereinfachen.

wir haben also:

$$\begin{eqnarray*} F(1,r_y-0.5) &=& r_y^2-r_x^2r_y+1/4\cdot r_x^2 \quad \mbox{ger... ...quad & \mbox{beide F\uml alle SE und Fall S} \end{array}\right. \end{eqnarray*}$$