Mittelpunkt-Entscheidungsalgorithmus

• betrachten nur den Fall, dass die Steigung im Intervall $[0,-1]$ liegt, d.h. nur ein Oktant wird gezeichnet
• verwenden nur ganzzahlige Additionen und Subtraktionen in der inneren Schleife
• nehmen an, Kreis liegt im Ursprung, und verschieben bei SetPixel()

andere Oktanten: Übung.

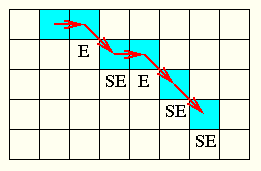
treffen sukkzessive Entscheidungen: liegt nächstes Pixel im Osten (E) oder im Südosten (SE) ?

untersuchen hierzu Mittelpunkt zwischen diesen beiden Pixel durch Einsetzen in die implizite Form

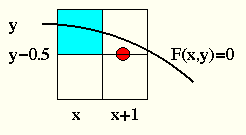
Wann beträgt die Steigung -1?

wenn $x=y$!

 
void DrawCircleOctant(
  int x0, int y0,
  int r
  int color
) {
  int x(0);
  int y(r);

  SetPixel(x+x0, y+y0, color);
  while( x < y ) {
    if( F(x+1, y-0.5) >= 0) y--;
    x++;
    SetPixel(x+x0, y+y0, color);
  }
}

Statt $F(x,y)$ immer wieder komplett zu berechen nutze bereits berechnete Werte aus vorhergehender Iteration!

Fall E:

$$\begin{eqnarray*} \lefteqn{F(x+2,y-0.5)-F(x+1,y-0.5)} \\ &=& (x+2)^2+(y-0.5)^... ...\mbox{}-(x+1)^2+(y-0.5)^2-r^2 \\ &=& 2x+3 \\ &=& 2(x+1)+1 \end{eqnarray*}$$

Die Berechnung von $F$ hängt weiterhin von $x$ ab, dies können wir aber auch inkrementell berechnen!

Fall SE:

$$\begin{eqnarray*} \lefteqn{F(x+2,y-1.5)-F(x+1,y-0.5)} \\ &=& (x+2)^2+(y-1.5)^... ...+1)^2+(y-0.5)^2-r^2 \\ &=& 2x-2y+5 \\ &=& 2(x+1)-2(y-1)+1 \end{eqnarray*}$$

Die Berechnung von $F$ hängt weiterhin von $x$ und $y$ ab, dies können wir aber auch inkrementell berechnen!

Zu Beginn:

$$\begin{eqnarray*} \lefteqn{F(1,r-0.5)} \\ &=& 1^2+(r-0.5)^2-r^2 \\ &=& 5/4-r \\ \end{eqnarray*}$$

Wählen $1-r$ (statt mit 4 zu multiplizieren).

Macht man dabei einen groben Fehler?: Übung.

wir haben also:

$$\begin{eqnarray*} F(1,r-0.5) &=& 1-r \\ \Delta F &=& \left\{\begin{array}{lcl... ...x{Fall E} \\ 2 & \quad & \mbox{Fall SE} \end{array}\right.\\ \end{eqnarray*}$$