Andere Steigungen: Übung.
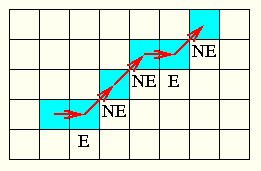
treffen sukkzessive Entscheidungen: liegt nächstes Pixel im Osten (E) oder im Nordosten (NE) ?
untersuchen hierzu Mittelpunkt zwischen diesen beiden Pixel durch Einsetzen in die implizite Form
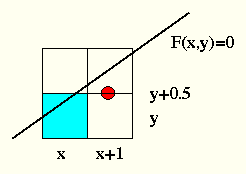
void RestrictedDrawLine(
int x0, int y0,
int x1, int y1,
int color
) {
int y(y0);
for(int x(x0); x!=x1+1; x++) {
SetPixel(x, y, color);
if( F(x+1, y+0.5) > 0 ) {
y = y+1;
}
}
}
Trick: Statt ![]() immer wieder komplett zu berechnen,
nutze bereits berechnete Werte aus vorhergehender Iteration!
immer wieder komplett zu berechnen,
nutze bereits berechnete Werte aus vorhergehender Iteration!
Berechnen wir die Differenz zweier aufeinander folgender Iterationen:
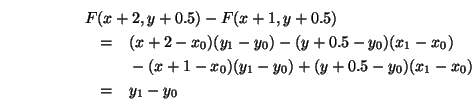


Wir wollen zu Beginn nicht mit ![]() multiplizieren, also:
multiplizieren, also:
Trick: Multipliziere ![]() mit 2, was beim Vergleich
mit 0 nichts ausmacht!
mit 2, was beim Vergleich
mit 0 nichts ausmacht!
void RestrictedDrawLine(
int x0, int y0,
int x1, int y1,
int color
) {
int y(y0);
for(int x(x0); x!=x1+1; x++) {
SetPixel(x, y, color);
if( 2 * F(x+1, y+0.5) > 0 ) {
y = y+1;
}
}
}
wir haben also:

d.h. insbesondere, dass das inkrementelle Aktualisieren
von ![]() nicht von
nicht von ![]() oder
oder ![]() abhängt, was man bei einer Geraden
auch intuitiv erwartet.
abhängt, was man bei einer Geraden
auch intuitiv erwartet.
also ergibt sich der: