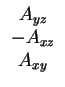
Si sabemos que todos los puntos están en un plano, un vector normal al plano se podría calcular sencillamente con:
¿En qué dirección apunta dicho vector?
Usamos una regla de la mano derecha para interpretar el producto vectorial:
Si el pulgar apunta en dirección del primer vector y el dedo índice apunta en dirección del segundo vector, entonces, el dedo medio apunta en direccion del vector del producto.
Por otro lado, si se puede seguir a tres vectores de esta manera con los dedos de la mano derecha, los vectores forman un sistema de coordenadas derecho.
Matemáticamente, eso se expresa de la siguiente forma:
Tres vectores (tridimensionales) a, b y c forman un sistema de coordenadas derecho si el producto mixto a(b x c) (es decir, el producto escalar entre a y el producto vectorial entre b y c) es mayor que cero (es decir, estrictamente positivo).
Sin embargo, calcular el vector normal de un polígono a base del producto vectorial no es recomendable por dos razones:
Miramos otra forma un poquito más compleja:
Dado un polígono tridimensional (por el momento asumimos que esté colocado en un solo plano), se puede calcular un vector normal N con la siguiente fórmula:
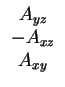
donde Axy (respectivamente Axz y Ayz) es el área de la proyección del polígono al plano xy (respectivamente xz e yz) del sistema de coordenadas.
Bueno, hemos pasado la pelota: en vez de calcular el vector normal tenemos que calcular áreas...