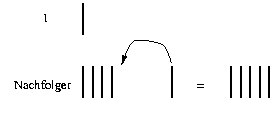
Natürliche Zahlen
Darstellungsmöglichkeiten für die natürlichen Zahlen (mit der Null)
Unär-Darstellung
Vereinbaren wir als Symbol für die Eins einen Strich, z.B. auf einem Blatt Papier. Den Nachfolger einer Zahl, d.h. einer Reihe von Strichen, erhalten wir dadurch, dass wir noch einen Strich hintendran malen.
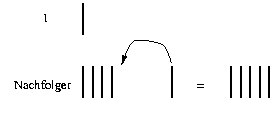
Wir haben nun aber keine Null, d.h. kein Symbol, welches wir hinschreiben können, wenn wir eigentlich nichts hinschreiben wollen.
Vereinbaren wir für die Null einen Kringel.
Wir können dann Zahlen in Unär-Darstellung wie folgt schreiben:
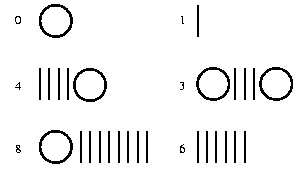
Unär dargestellte Zahlen haben die recht unangenehme Eigenschaft, dass sie sehr lang werden können, was uns ungemein beim Geldverdienen und Geldausgeben stört, da wir die meiste Zeit damit beschäftigt wären, allein die Steuern richtig zu notieren.
Zudem führt das Hinschreiben der Symbole für die Null zu mehrdeutigen Darstellungen für die Zahlen.
Binär-Darstellung
Vereinbaren wir folgendes:
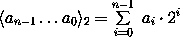
|
Mit den indizierten a's bezeichnen wir die Ziffern, die von rechts nach links beginnend mit Null durchnummeriert sind.
Insbesondere bedeutet dies, dass wir die Zahlen (z.B. als Geld) nicht mehr einfach wie eine Menge Steine in einem Sack mit uns herum tragen können, da es jetzt auf die Anordnung der Ziffern ankommt.
p-när-Darstellung
Das Ganze klappt auch mit mehr Symbolen (also Fast-Chinesisch ...). Üblicherweise benutzen wir neben dem Dualsystem auch das Zehnersystem, das Hexadezimalsystem, und das Oktalsystem mit den folgenden Symbolen für die Ziffern:

|
Damit das ganze funktioniert, muss eine Zahl eindeutig in Ziffern zerlegbar sein. Ferner sei bemerkt, dass diese p-näre Zahlendarstellung eindeutig ist, d.h. zu gegebener Basis (und gewählten Ziffern) hat jede natürliche Zahl genau eine Zahlendarstellung zu dieser Basis. (Bemerkung: Dies müsste man beweisen.)
Die Zahl berechnet sich dann analog wie bei der Binär-Darstellung mit folgender Formel, wobei b die Basis angibt:
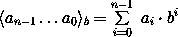
|
Beachte: wir müssen dazu schon wissen, was Addieren und Multiplizieren ist, und was die abkürzende Schreibweise mit Exponenten bedeutet. Das wissen wir aber bereits aus der Schule (oder wir machen es wie die Ägypter mit Steinen). Weiterhin stehen die a's links vom Gleichheitszeichen für Ziffern, rechts dagegen für Zahlen! Diesen feinen kleinen Unterschied wollen wir allerdings nicht vertiefen.
Natürlich schreiben wir in Zukunft Zahlen im Zehnersystem wie gewohnt ohne spitze Klammern und Index und unterscheiden nicht zwischen der Darstellung der Zahl und der dargestellten Zahl. Das mit der 10 hat wohl nur den besonderen Grund, dass wir 10 Finger haben.
Was haben wir gewonnen?
Betrachten wir die Längen der Darstellungen:

Also:
0x39A7B und Oktalzahlen
sind durch eine führende Null gekennzeichnet;
dies kann leicht zu Verwirrung führen!)
Negative Zahlen
Insbesondere wenn man Schulden hat oder macht, sollte man auch mit negativen Zahlen rechnen können. Außerdem erleichtern sie es, algebraische Strukturen zu definieren, und mit denen zu rechnen (wir wollten ja Algorithmen entwickeln!). Wir erweitern also unsere Vorstellung von natürlichen Zahlen zu den sogenannten ganzen Zahlen, die sowohl die natürlichen als auch die negativen Zahlen umfassen (die Null ist natürlich auch dabei, da wir diese bereis zu den natürlichen Zahlen zählen).
Darstellungsmöglichkeiten für die ganzen Zahlen
Negative Zahlen mit Betrag und Vorzeichen
Wir könnten natürlich für das Vorzeichen ein neues Symbol einführen (so wie wir es aus der Schule gewohnt sind, z.B. ein Minus-Zeichen zu verwenden), allerdings können wir auch die Darstellung mit Strichen und Kringeln neu interpretieren.
Das linkeste Symbol in einer Zeichenreihe gibt an,
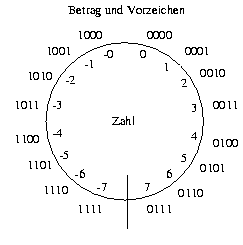
Wir sehen:
Bemerkung: Diese Darstellung funktioniert auch in Unär-Darstellung. Wenn ein Kringel vorhanden ist (egal wo), sagen wir, die Zahl ist negativ, ansonsten positiv. Dann gibt es dort nur eine Null, nämlich wenn nur ein Kringel vorhanden ist.
Negative Zahlen im Zweier-Komplement
Wir schreiben ebenfalls Zeichenfolgen von 0en und 1en und interpretieren wie folgt:
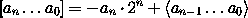
|
Beispiel für eine 7-bit Zahl im Zweier-Komplement:
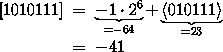
Veranschaulichung der Darstellung durch einen Zahlenkreis, innen die dargestellte Zahl (in der gewohnten Dezimalschreibweise), außen die Darstellung mit Zeichenfolgen (mit 0en und 1en):
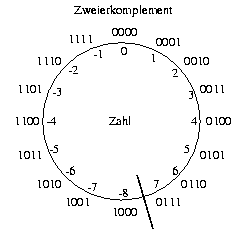
Wir sehen:
Wie erhalten wir die Darstellung einer Zahl, die wir mit Betrag und Vorzeichen kennen, im Zweier-Komplement?
Trick: wir nehmen das Einer-Komplement des Betrags und addieren noch eins drauf.
Genauer:

Das rechnen wir mal nach:
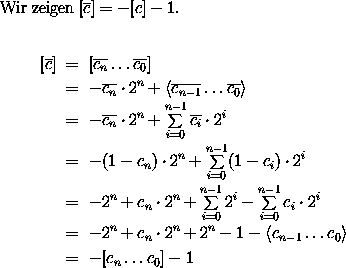
Wir haben hier schon eine Menge von Regeln zum Manipulieren der Zahlen und Formeln benutzt, zum Glück kennen einige davon schon aus der Schule und andere können wir zur Not in einer Formelsammlung nachlesen.
Bemerkung: Zahlen im Zweier-Komplement sind nicht mehr so einfach miteinander zu vergleichen.
Die Methode der Komplementbildung kann man auch auf p-när dargestellte Zahlen erweitern. Man spricht dann z.B. vom Zehner-Komplement und vom Neuner-Komplement anstelle des Zweier- und Einer-Komplements.
Negative Zahlen in Bias-Darstellung
Wir spannen die Darstellung durch die Addition eines Wertes vor, d.h. wir erhalten die Zahl, indem wir diesen Wert wieder subtrahieren.
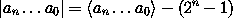
|
Wir notieren Zahlen in Bias-Darstellung durch Klammerung mit senkrechten Strichen.
Veranschaulichung der Darstellung durch einen Zahlenkreis, innen die dargestellte Zahl (in der gewohnten Dezimalschreibweise), außen die Darstellung mit Zeichenfolgen (mit 0en und 1en):
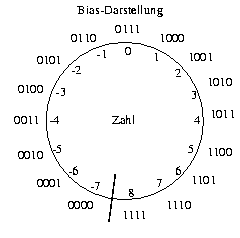
Zahlen in Bias-Darstellung sind wieder einfach miteinander zu vergleichen.
Modulo-Darstellung
Wir kennen die Primzahlen, das waren die Zahlen, die wir nur durch Eins und durch sich selbst ohne Rest teilen konnten.
Können wir die Primzahlen für eine eigenartige Darstellung der Zahlen verwenden?
Arbeiten wir mit einem Beispiel. Nehmen wir uns eine Menge von Primzahlen, z.B. 2,3,5 und 7.
Wir notieren eine Zahl im Interval [0:2*3*5*7-1]=[0:209], d.h. von 0 bis zum Produkt aller Primzahlen minus 1, durch die Angabe der Reste, wenn wir die Zahl durch die Primzahlen teilen. Dabei verwenden wir geklammerte Zeichenfolgen mit Kommas zum Abtrennen der Blöcke.
Z.B: 68 ist (5,3,2,0)
Der umgekehrte Schritt ist ein wenig komplizierter. Wir benötigen den euklidschen Algorithmus zum Auffinden des größten gemeinsamen Teilers und einiges Wissen über diophantische Gleichungen. Dies wollen wir hier nicht weiter ausführen.
Machen wir hier nur ein Beispiel zum Rechnen in dieser Zahlendarstellung.

Wir wollen diese Umrechnung hier nicht weiter vertiefen, da wir sie im Folgenden nicht brauchen. Wir wollen nur festhalten: es ist nicht ganz einfach.
Allerdings sind drei Dinge zu bemerken:
Da mussten wir eine Menge tun, damit wir ordentlich mit Zahlen handtieren können und keine riesigen Zahlendarstellungen mit uns herum tragen müssen. Fassen wir nochmal zusammen:

|
Gleitkommazahlen
Neben den natürlichen Zahlen und den ganzen Zahlen, gibt es noch eine Menge anderer Zahlen:
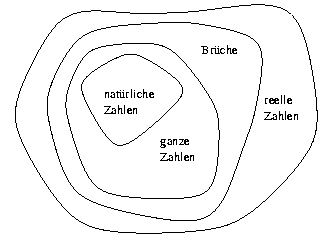
Rationale Zahlen, d.h. die Brüche, kann man noch genau darstellen, sofern man sich genügend Bits spendiert; dies ist i.A. bei reellen Zahlen jedoch nicht mehr möglich.

|
Um nun diese Zahlen zumindest näherungsweise darstellen zu können (und nicht wieder ellenlange Folgen von Nullen schreiben zu müssen) schreiben wir die Zahlen mit
Beispiel mit der Basis 10:

|
Als Formel:

|
Beachte: Wir haben hier die Bits von links nach rechts nummeriert! Zudem benutzt der IEEE-Standard die Bias-Darstellung für den Exponenten, um so auch Verschiebungen des Kommas nach links bewirken zu können, und trotzdem den Vergleich zweier Exponenten in Funktionseinheiten leicht zu gestalten.
Wir schreiben also mindestens eine von Null verschiedene Stelle vor das Komma! Da wir diese immer schreiben, können wir sie bei der Schreibweise zur Basis 2 auch weglassen und immer bei der Interpretation der Zahl automatisch einfügen.
Problem: damit haben wir keine Null mehr.
Eine Lösung, die fast alle Computer der Welt nutzen (macht halt das Austauschen von Daten einfacher), ist das IEEE-Format.
IEEE-Format
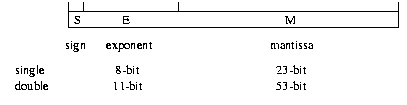

|
Vorteile der Darstellung:
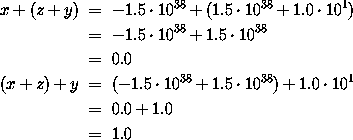
|
Wir halten nochmal fest:
Entscheidend ist also nicht die Zeichenfolge an sich, sondern deren Interpretation durch die angewendeten Operationen!