
Digitale Zustände: es gibt nur Null und Eins und die Zeit. Null und Eins muss interpretiert und realisiert werden. Entweder high oder low wird als logische Null oder Eins interpretiert (high=1: positive Logik, `active high logic'); high=0: negative Logik, `active low logic').
Schaltfunktionen
Frischen wir erst Altbekanntes auf.
Wir interessieren uns für Schaltnetze mit nur einem Ausgang und n Eingängen, die wir mit Indizes durchnummerieren. Jeder Eingang und auch der Ausgang soll nur einen der beiden Zustände annehmen können. Der Ausgang soll allein durch die Eingangsbelegung festgelegt sein.

Einfache Schaltfunktionen mit zwei Eingängen sind die UND-, die ODER- und die NICHT-Funktion:

|
Man realisiert diese Schaltfunktionen durch sogenannte logische Gatter oder gates mit den folgenden Schaltsymbolen:
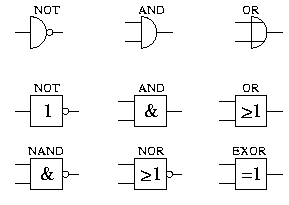
Alle Schaltfunktionen, die mit zwei Eingängen zu realisieren sind zeigt folgende Tabelle (einige sind auch als Symbole oben dargestellt, hier erscheinen die englischen Namen):
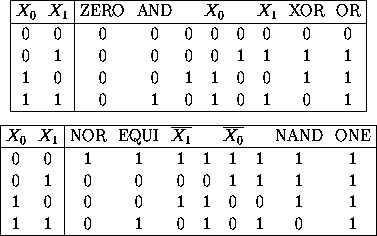
|
Betrachten wir zur Auffrischung der Kenntnisse die Konstruktion einer einfachen Schaltung. Wir wollen mithilfe der ägyptischen Zahlendarstellung (hier einer geordneten Unär-Darstellung) eine moderne Siebensegmentanzeige ansteuern (dabei verzichten wir auf die Null).
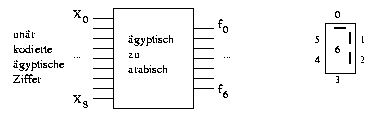
Man erhält mit den Vereinbarungen aus der Abbildung folgende Wertetabelle:

|
Damit ergibt sich z.B. die VDNF (vollständige disjunktive Normalform) für die Funktion zur Ansteuerung des oberen Segmentelements zu:

|
Die weiteren Funktionen erhält man auf analoge Art und Weise. Eine VKNF (vollständige konjunktive Normalform) wäre an dieser Stelle wegen der vielen Nullen sehr teuer. Die heute gebräuchlichere Umsetzung geht von einer Binär-Darstellung (sogenannter binär kodierter Dezimalzahlen oder einfach BCD-Zahlen) aus. Man benötigt 4 Bit, kann damit aber sogar 16 Ziffern kodieren. Wir nehmen an, dass nur 10 Ziffern umgesetzt werden (eine Erweiterung auf die Hexadezimalzahlen ist einfach), die nicht erlaubten Ziffern dürfen eine beliebige Anzeige erzeugen.
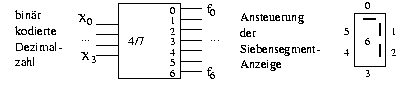
Die Wertetabelle (nun einschließlich einer Null!) sieht wie folgt aus:

|
Da oft weniger 0en als 1en vorkommen, empfehlen sich für viele der Funktionen die VKNFs, z.B. (man wählt die freien Einträge entsprechend als 1en):
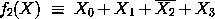
|
Rekursives Schaltungsdesign
Wir gehen im Folgenden nicht auf Minimierungsverfahren zur Reduktion der Kosten eines Schaltkreises ein. Zu den bekannten Verfahren gehören die Methoden von Quine-McClusky oder die Veitch- bzw. Karnaugh-Diagramme. Vielmehr konzentrieren wir uns auf die rekursive Konstruktion regelmäßiger Funktionseinheiten.
Wiederholen wir aber zuerst, was unter Kosten und Tiefe der Realisierung einer Schaltfunktion zu verstehen ist.
Kosten und Tiefe
Wir haben Schaltfunktionen auf zwei Arten realisiert:
Für die Tiefe T vereinbaren wir z.B. folgendes:
Nicht zykelfreier Graph (damit keine Repräsentation eines Schaltkreises):

Zykelfreier Graph mit Angabe der Tiefe der Knoten:

Eine topologische Sortierung der Knoten ist z.B. gegeben durch: 1,7,6,2,4,3,5,8.
Beachte: bei diesen Definitionen für Kosten und Tiefe wurden die Verbindungen zwischen den Gattern nicht berücksichtigt!
Decoder
Ein Decoder ist ein Schaltkreis, der je nach Wert (Interpretation als Binärzahl) am Eingang, genau einen Ausgang auf 1 setzt.
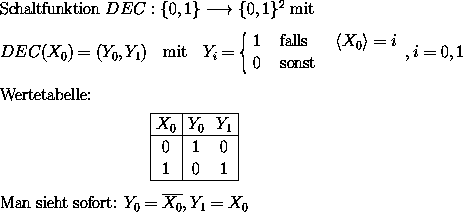


Realisierung mit Normalformen
Man kann nun den Decoder mithilfe der Normalformen realisieren, wobei sich für n=8 die Kosten zu 2*8+8*3/2=28 ergeben. Allgemein gilt für die Kosten:
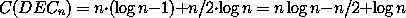
da jeder der n Minterme log(n)-1 viele UND-Gatter und insgesamt genauso viele NICHT-Gatter wie Nullen auf der linken Seite der Tabelle vorkommen.
Die Anzahl der Inverter kann reduziert werden, da jede Schaltvariable nur einmal negiert werden muss; es sind also lediglich log(n) viele NICHT-Gatter erforderlich. Also:
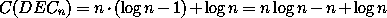
|
Wie tief ist diese Konstruktion?
Es kommt darauf an, wie geschickt wir die Minterme realisieren. Bei vier Variablen gibt es z.B. die folgenden Möglichkeiten:
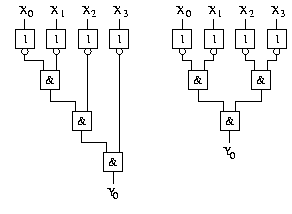
Wir können also eine Tiefe von 3 erhalten. Allgemein erhalten wir für die Tiefe eines n-Decoders:

|
Schaltsymbol des n-Decoder (d.h. die Größe wird durch die Anzahl der Ausgänge bestimmt):

Wir haben also viele verschiedene Darstellungen für den gleichen Sachverhalt, nämlich der Beschreibung einer Schaltfunktion:
Rekursive Realisierung
Nehmen wir an, wir hätten schon einen n-Decoder realisiert. Wir wollen nun mit zwei solchen und einigen weiteren Gattern einen 2n-Decoder zusammenbauen.
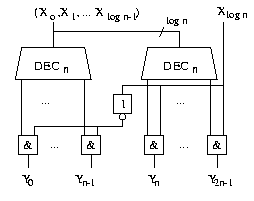
(Bemerkung: diese Schaltung ist offensichtlich nicht die schlauste; man kann auch einfach nur einen n-Decoder verwenden, aber trotzdem ist sie korrekt und wir können Kosten und Tiefe berechnen. Später sehen wir die einfachere Schaltung.) Wie berechnen wir nun aber Kosten und Tiefe?
Rekursionsformeln
Wir lernen hier zwei einfache Rekursionsgleichungen kennen, die uns sehr nützlich sein werden. Die Idee dahinter ist recht einfach zu verstehen (hier sehr informal):
Gegeben ein Problem der Großenordnung n (was immer das bedeuten mag), kennt man die Lösung des Problems kleinerer Ordnung sowie eine Konstruktion, wie man mithilfe dieser kleineren Lösung, die Lösung für das große Problem erhält, so kann man den Aufwand mithilfe der Rekursionsgleichung berechnen. Das kleinere Problem kann einfach von der Größenordnung n-1 sein (lineare Rekursion), oder aber lediglich von der Größenordnung n/b, d.h. dem b-ten Teil, sein (logarithmische Rekursion).
Verwenden wir die folgenden Bezeichnungen:

|
Formeln für die logarithmische Rekursion:

|
Betrachten wir nochmals den oben bereits gezeigten 2n-Decoder:

Die Parameter für die logarithmische Rekursionsgleichung ergeben sich zu:

|
Für die Kosten des rekursiv definierten 2n-Decoders erhalten wir also:

Und somit als Kosten eines n-Decoders:

|
Es ist eine schöne Übung, das Ergebnis konkret für einen 4- und 8-Decoder nachzurechnen.
Nun haben wir schon bemerkt, dass die Konstruktion nicht die geschickteste war. Wir können ja einfach einen der beiden n-Decoder weglassen. Tun wir dies.
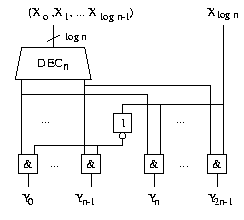
Die Parameter für die logarithmische Rekursionsgleichung sind damit wie folgt:

|
und die Kosten berechnen sich nun zu:
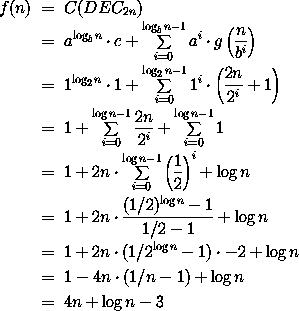
womit sich für einen n-Decoder Kosten ergeben, die um einen Faktor log(n) niedriger liegen als in der vorhergehenden Konstruktion:

|
Schauen wir uns nun die Tiefe unserer Konstruktionen an. Die Tiefen beider Konstruktionen sind offensichtlich identisch. Berechnen wir die Tiefe der Decoder ebenfalls mit der Rekursionsformel.

womit sich die Tiefe eines 2n-Decoders mit folgenden Parametern

|
wie folgt berechnet
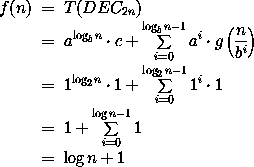
Die Tiefe eines n-Decoders beträgt also
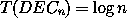
|
was deutlich mehr als die log(log(n)) von der Konstruktion mit der Normalform ist.
Geben wir uns also damit zufrieden? Nein!
In obigen Konstruktionen haben wir die Größe der Decoder bezüglich der Ausgänge bestimmt. Wiederholen wir kurz die Diskussion, nun allerdings bestimmen wir die Größe bezüglich der Eingänge.

Nun nutzen wir die Formel der linearen Rekursion und erhalten mit den Parametern:

|
folgende Kosten:
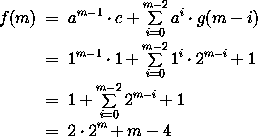
Wie nicht anders zu erwarten, erhalten wir die gleichen Kosten wie oben, wenn wir für m wieder log(n) einsetzen.
Nun stellt sich die Frage, ob nicht auch eine logarithmische Konstruktion möglich ist. Nehmen wir an m sei eine Zweierpotenz.

Die Parameter der Rekursionsgleichung für die Kosten ergeben sich als:

|
und damit erhalten wir die folgende Gleichung
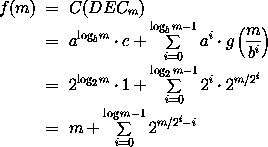
die allerdings nicht ganz so einfach zu einer einfachen geschlossenen Formel aufzulösen ist. Allerdings kann man zeigen, dass für wachsende m gilt:

Die verbesserte Konstruktion kostet also für hinreichend große m ungefähr die Häfte.
Betrachten wir nun die Tiefe der neuen Konstruktion. Die Parameter der Rekursionsgleichung für die Tiefe ergeben sich als:

|
und wir erhalten die gleiche Tiefe wie bei der Konstruktion mit der Normalform (allerdings bei erheblich geringeren Kosten):
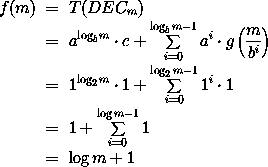
Fassen wir die Ergebnisse der verschiedenen Konstruktionen nochmals zusammen (wir betrachten wieder als Grundlage für die Größe die Anzahl der Ausgänge):

|
Vergleicher
Wenden wir die rekursive Konstruktionsmethode an, um Vergleicher zu bauen.
Ein Vergleicher ist ein Schaltkreis, der zwei Eingangssignale miteinander vergleicht und genau einen Ausgang auf 1 setzt, je nachdem, ob der Vergleich kleiner, gleich oder größer ergibt.

Dies ergibt folgende Wertetabelle:

|
Wir sehen sofort die Schaltfunktionen sowie eine mögliche Realisierung mit den sich ergebenden Kosten und Tiefe:
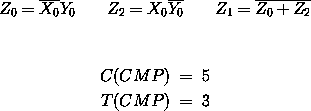

Will man zwei n-stellige Binärdarstellungen zweier Zahlen miteinander vergleichen, muss man folgende Schaltfunktion realisieren.
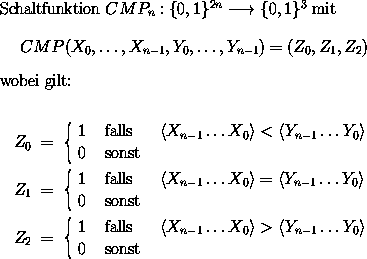
Nun gilt aber offensichtlich folgendes (schreiben wir hierzu abkürzend für die beiden n-stelligen Eingänge X und Y):
X ist kleiner als Y, wenn bereits die oberste Stelle kleiner ist. X ist größer als Y, wenn bereits die oberste Stelle größer ist. Sind die beiden obersten Stellen gleich, so entscheiden allein die unteren Stellen.
Wir können also einen n-Vergleicher wie folgt aufbauen:
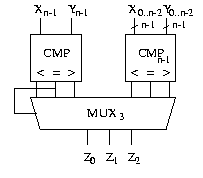
Wir wenden die Formel der linearen Rekursion an und erhalten mit den Parametern für die Kosten und die Tiefe:

|
die folgenden Kosten bzw. Tiefe:
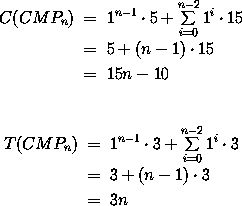
Beachte: auch hier konnte man das eigentlich notwendige Maximum über beide Pfade eliminieren, da stets gilt:
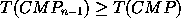
Die obige Konstruktion benutzt nur das oberste Bit für die Rekursion. Es gilt aber doch auch die allgemeinere Form:

Die anderen Fälle für gleich und größer gelten analog. Lassen wir für n nur Zweierpotenzen zu, so können wir den n-Vergleicher durch folgende Konstruktion realisieren:
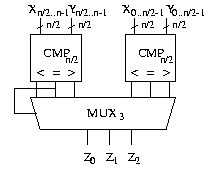
Das heißt, wir vergleichen zuerst die oberen und die unteren Hälften der Eingabewerte und entscheiden anschließend über das Resultat. Für die Kosten und die Tiefe ergeben sich nun mit den Parametern

|
die folgenden Lösungen (jetzt logarithmische Rekursion):
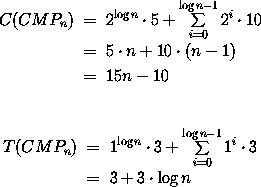
Die Kosten haben sich also nicht verändert, was wir auch genau so erwartet haben. Die Tiefe hat sich jedoch von linearer auf logarithmische Größenordnung reduziert.
Mit der gleichen Methode lassen sich auch viele andere regelmäßige Basisfunktionseinheiten aufbauen. Beispiele sind: