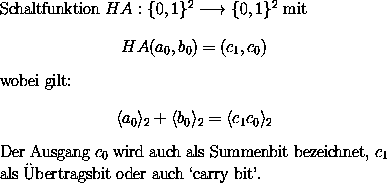
Halbaddierer
Ein Halbaddierer realisiert eine 1-stellige Addition zweier Binärzahlen.
Wertetabelle:

|
Die Schaltfunktionen können direkt mit jeweils einem Gatter (also Kosten 2 und Tiefe 1) realisiert werden.

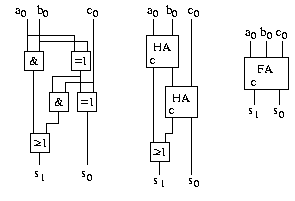
Volladdierer
Ein Volladdierer realisiert eine 1-stellige Addition zweier Binärzahlen mit Eingangsübertrag.

d.h. wir müssen folgende Wertetabelle realisieren:

|
Dies ist mit einfachen Ausdrücken möglich, was folgende Schaltung mit Kosten 5 und Tiefe 3 zeigt:
n-Bit Addierer
Wir haben gesehen, dass es verschiedene Möglichkeiten gibt, einen Schaltkreis aufzubauen. Man kann versuchen, die Kosten oder die Tiefe des Schaltkreises zu minimieren. Es ergibt sich häufig ein trade-off zwischen Kosten und Tiefe und man muss sich je nach Gegebenheit für eine Variante entscheiden. Wir wollen im Folgenden einige Addierer kennen lernen, die sich bezüglich Kosten und Tiefe zum Teil erheblich unterscheiden.
Zuerst die formale Definition eines Addierers. Ein n-Bit Addierer realisiert eine n-stellige Addition zweier Binärzahlen mit Eingangsübertrag.

Insbesondere gibt es je Stelle nur ein Übertragsbit, welches sich gerade auf die nachfolgende Stelle auswirkt (d.h. eins im Sinn hat seinen Sinn).
Wir wollen im Folgenden auf formale Beweise der Korrektheit der Addierer verzichten. Der Leser sei jedoch gewarnt, man muss diese Beweise führen.
Ripple Carry Addierer (RCA)
Der erste Addierer arbeitet nach der Schulmethode.
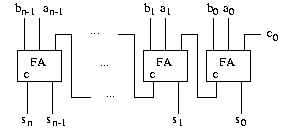
Von rechts nach links werden die entsprechenden Bits und der Übertrag der vorhergehenden Stellen addiert. (Das Bild verdeutlicht auch, weshalb der Addierer Ripple Carry Addierer heißt: ripples sind kleine regelmäßige Wellen, auf deutsch müsste man Kräuseladdierer sagen.) Der Ripple Carry Addierer wird auch häufig Carry Chain Addierer genannt. Den Eingangsübertrag der gesamten Schaltung belegt man mit 0. Ist das oberste Bit der Summe gleich 1, so ist die Summe nicht mehr als n-Bit Zahl darstellbar.
Wir können den RCA auch mit folgender Konstruktion rekursiv realisieren:

Ohne jetzt explizit die Formel der linearen Rekursion anzuwenden, erkennen wir, dass die Kosten und die Tiefe eines n-Bit RCAs sich zu folgenden Werten berechnen:
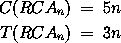
Lassen wir wieder nur Zweierpotenzen für die Länge der Eingabezahlen zu, so können wir einen wesentlich schneller addierenden Schaltkreis entwerfen.
Conditional Sum Addierer (CSA)
Sei n im Folgenden eine Zweierpotenz.
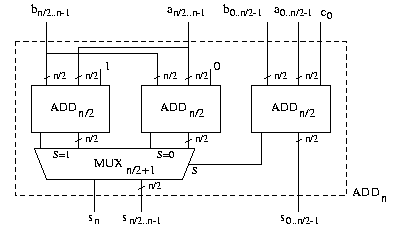
Die Kosten des CSA berechnen sich gemäß der Formel
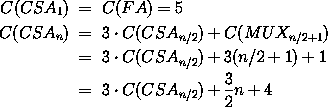
Was zu den folgenden Parametern für die Kosten und die Tiefe führt:
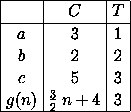
|
Damit erhalten wir (unter Verwendung der geometrischen Reihe und einiger Potenzrechenregeln):
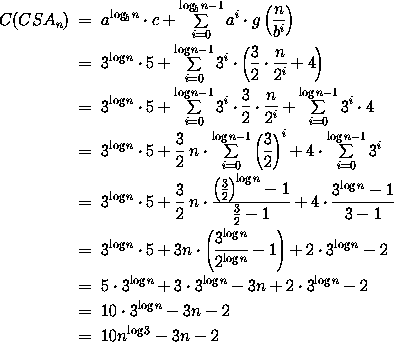
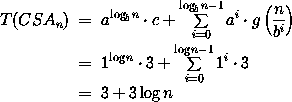
Er ist also um einiges teurer aber wesentlich schneller als der RCA. Wir können den CSA jedoch noch erheblich verbessern, wie der folgende Abschnitt erläutert.
Two Sum Addierer (TSA)
Wir haben beim CSA gesehen, dass es sich ausgezahlt hat, beide Möglichkeiten - also ein Übertrag von rechts bzw. kein Übertrag von rechts - vorzuberechnen.
Bauen wir mit dieser Methode gleich einen ganzen Addierer, der generell stets beide Summen berechnet. Dies scheint ein Mehraufwand zu bedeuten, wir werden aber sehen, dass der Addierer nicht zu teuer, aber sehr schnell ist.
Beginnen wir wieder mit einer 1-Bit Version:
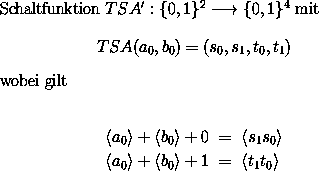
Wertetabelle

|
Und wir sehen sofort
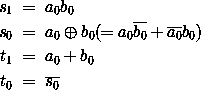
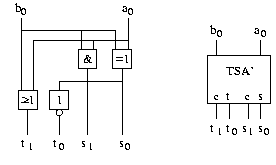
Die Kosten betragen also 4 und die Tiefe beträgt 2. Nun konstruieren wir rekursiv einen n-stelligen TSA'. Nehmen wir an, wir hätten zwei n/2 TSA', die die beiden Summen für die obere und die untere Hälfte der Eingabezahlen berechnen. Die untere Hälfte der Ausgabe wird nur durch den unteren TSA' bestimmt. Die obere Hälfte der Ausgabe wählen wir entsprechend des entstehenden Übertrags an der unteren Hälfte aus.
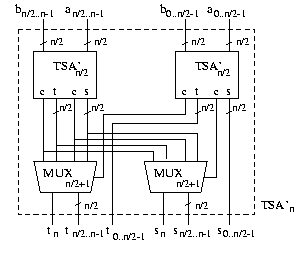
Bestimmen wir wieder wie schon gewohnt die Kosten und die Tiefe der TSA' Addierer mithilfe der Rekursionsformeln. Die Konstruktion liefert folgende Formel für die Kosten:
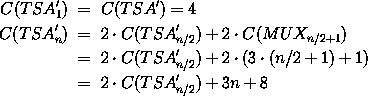
Die Parameter für die Rekursionsformeln sind also (bis auf die Konstante c ergeben sich die gleichen Parameter für die Tiefe wie oben beim CSA):
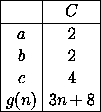
|
Und damit
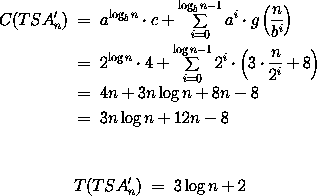
Da wir am Ende noch mithilfe des Eingangsübertrags die eigentlich gewollte Summe selektieren müssen, ergibt sich der gewünschte Addierer TSA aus einem TSA' durch Anbauen eines weiteren Multiplexers.
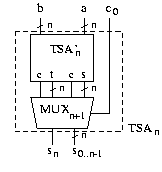
Und wir erhalten für die Kosten und die Tiefe letztendlich:
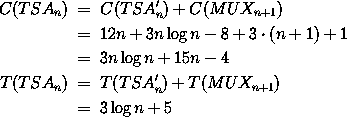
Block Carry Addierer (BCA)
Wir wollen einen weiteren recht billigen Addierer kennen lernen, der nicht ganz so schnell wie obige CSA bzw. RCA ist, allerdings wesentlich billiger. Er arbeitet ebenfalls nach dem Zwei-Summen-Prinzip und nutzt den Trick, die zu addierenden Zahlen so in Blöcke einzuteilen, dass die Berechnung des Übertrags der vorhergehenden Blöcke gerade ungefähr so lange dauert wie die Berechnung der Summe des aktuellen Blocks. Man betrachte den folgenden Ausschnitt aus einem Schaltkreis.
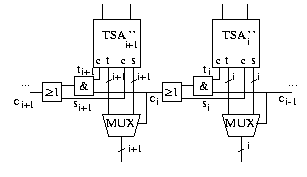
Das Selektsignal $c_i$ für den Block $i+1$ berechnet sich als

Wählen wir die Blockgröße so, dass deren Länge stets um 1 wächst, so erhalten wir folgende Einteilung der Zahlen. Die Tabelle gibt die Blockgröße, die gleich der Blocknummer ist, und die maximale Länge $n$ der Zahl an.

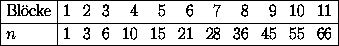
|

Wir wollen den BCA geschickt aufbauen, so dass die Tiefe in einem Block i, die den Selekteingang der Stufe i+1 bestimmt, gerade ungefähr gleich der Tiefe des dortigen TSA'' ist. Es soll also gelten
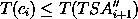
Nun gilt für die Tiefe dieses Selekteingangs
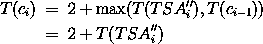
d.h. wenn wir als spezielle Two Sum Addierer TSA'' gerade einfache RCAs - einen für jede zu berechnende Summe - nehmen, haben wir die Bedingung erfüllt und es gilt:
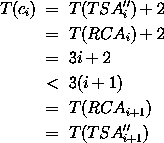
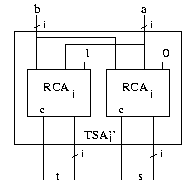
Damit ist aber die Tiefe eines BCA durch die Tiefe seines größten Blocks und des nachfolgenden Multiplexers bestimmt und wir erhalten:
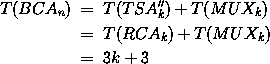
Berechnen wir die Kosten.
Wir benötigen für jeden Block zwei RCA, einen Multiplexer, der die korrekte Summe auswählt und - außer für den letzten Block - die beiden Gatter für die Übertragsweitergabe. Es ergibt sich also
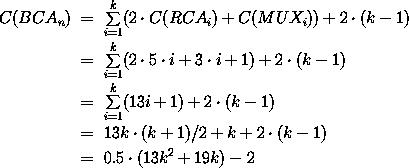
Mit obiger Abschätzung für k ergibt sich also abschließend
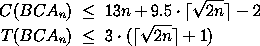
Carry Lookahead Addierer (CLA)
Der CLA ist theoretisch und auch in vielen Fällen praktisch der beste Addierer, insbesondere, wenn große Zahlen addiert werden sollen und Verdrahtung nicht dominierend wirkt.
Die Idee dieses Addierers besteht darin, parallel für alle Stellen des Addierers gleichzeitig zu berechnen, ob eine Stelle einen Übertrag generiert oder propagiert. Dies haben wir bereits beim BCA kennen gelernt. Man beobachtet nun, dass die Berechnung der beiden Signale carry-generate und carry-propagate für jede Stelle als assoziative Verknüpfung aufgefasst werden kann. Mithilfe eines parallel-prefix Schaltkreises können dann alle diese Signale mit Kosten linear in Anzahl der Stellen und Tiefe logarithmisch in Anzahl der Stellen berechnet werden.
Wir möchten an dieser Stelle jedoch nicht genau auf diesen wichtigen Addierer und das dahinterstehende Konzept eingehen, sondern lediglich Kosten und Tiefe mit angeben.
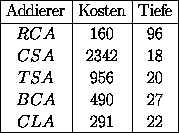
Zusammenfassung der Addierer
Folgende Tabelle fasst die Kosten und die Tiefe der verschiedenen Addierer einer Breite n zusammen:

|
Damit ergibt sich für 32-Bit Addierer:
|
Man beachte, dass diese Formeln so nur für das angegebene Kostenmaß (nämlich pro verwendetem Gatter 1) gelten.
Die verschiedenen Konzepte der Addierer können je nach Anforderungen der zu realisierenden Schaltung auch kombiniert angewendet werden. So kann man sich z.B. vorstellen aus 4-Bit Addierern, die schon als sogenannte Macros auf einem Chip vom Hersteller vorliegen, einen 32-Bit CSA zusammenzubauen, der dabei jedoch nur 15 der Macros verwendet und den Rest nach dem Zwei-Summen-Prinzip über Multiplexer verdrahtet.
Subtrahierer
Als erstes sei bemerkt: wir können einen Subtrahierer mit der gleichen Methodik wie einen Addierer aufbauen: Realisierung eines Halbsubtrahierers, Realisierung eines Vollsubtrahierers, der den borrow (den, den man im Sinn hat) berücksichtigt; und dann z.B. Realisierung eines Ripple Borrow Subtrahieriers, der genau nach der Schulmethode arbeitet.
Versuchen Sie dies zu tun! Beachten Sie, dass wir noch keine besondere Kennzeichnung der negativen Zahlen festgelegt haben. Bis jetzt argumentierten wir einfach mit Betrag und Vorzeichen!
Wir könnten also Zahlen in Darstellung mit Betrag und Vorzeichen addieren bzw.\ subtrahieren, was aber zwei Einheiten und eine spezielle Auswahlschaltung erforderlich machen würde.
Es gibt aber auch eine geschicktere Methode unter Verwendung der Darstellung im Zweierkomplement.

Mit anderen Worten, um zu subtrahieren, invertieren wir b bitweise, addieren a wie gewohnt und setzen dabei den Eingangsübertrag auf 1. Nun sehen wir auch ein, weshalb wir diesen Eingangsübertrag bei obigen Addierern stets berücksichtigt haben.
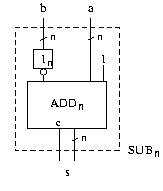
Ersetzen wir die NOT-Gatter durch XOR-Gatter, so erhalten wir einen Schaltkreis, der im Zweierkomplement sowohl addieren als auch subtrahieren kann.
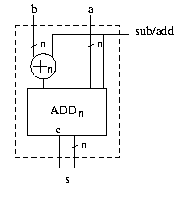
Weitere kurz angesprochene Themen waren: